【CFD/Python】移流項【CFDプログラミング講座 #2】

この講座ではPythonを使用したCFDプログラミングを解説していきます。最後まで受講して頂くと、差分法による流体解析ができるようになるようにしています。ぜひ最後までお付き合いください。

第二回からは移流項に関する解説をしていきます。移流項は最も難しい部分ですが、特に重要なので先に解説します。

前回の第一回ではナビエ・ストークス方程式の全体像を掴みました。CFDは難しいイメージがありますが、核の部分はシンプルです。まだ見てない方は下記からどうぞ。

【CFD/Python】ナビエ・ストークス方程式【CFDプログラミング講座　#1】

CFDとナビエ・ストークス方程式

まずはナビエ・ストークス方程式について軽く振り返りましょう。

CFDは流体の流れを解析によって予測します。つまり、現在の結果と物理の計算結果から、未来の結果を予想するということです。

CFDでは流れの予測にナビエ・ストークス方程式を使用します。ナビエ・ストークス方程式は下記のような式になります。

項が多くて複雑そうに見えますが、それぞれ物理的な意味を持っています。そのため、分解して考えることができます。第二回からはしばらく左辺第二項の移流項に関する説明を進めていきますのでお付き合いください。

移流項とは？

移流項は移動を表す項です。川の水は流れに沿って上流から下流に流れていきますが、全ての流体は流速に沿った流れの影響を受けます。

当たり前のように思えるかもしれませんが、粘性や重力、遠心力等の外力があると流体が流れる向きが時々刻々と変わリます。流体の動きが複雑なので、ナビエ・ストークス方程式は複雑になっているわけです。

ここからの移流項の解説では、単純化のために粘性力や外力の影響を無視して考えていきます。圧力も無視するため、ナビエ・ストークス方程式は下記のように変形できます。

$$ \frac{\partial v}{\partial t} + (v \cdot \nabla)v = 0$$

このような非定常項と移流項の関係式を移流方程式と呼びます。ただ、この式だと移動する物性値ｖと移動する速度ｖが同じなので、非線形方程式になります。

流体は、速度だけではなく熱やVOF値も運びます。そのため、適用範囲を広げるために移流方程式を線形にします。移動する物性値 u 、速度 c とすると下記のような式になります。

$$ \frac{\partial v}{\partial t} + c \frac{\partial v}{\partial x} = 0$$

ここまで単純化することで、時間とともに流体が物性値を運ぶ様子だけを捉えることができます。

下記は物性値を運ぶ様子をプロットした図です。初期条件では物性値uはx=0.5~1.0の範囲でu=1、それ以外では0を与えています。移流方程式を解くことで、物性値が流れ方向に進むことがわかります。

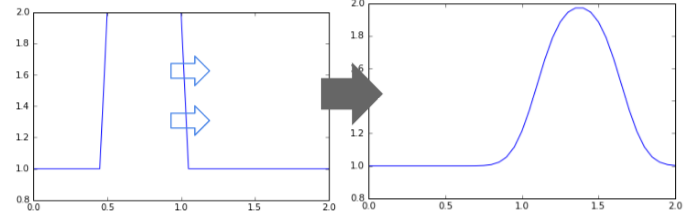
ここで問題が一つあります。移流方程式を正しく解けた場合は、本来は波の形状がそのまま移動するはずです。しかし、上の図では波の形が矩形波から滑らかな形に変化してしまっています。

これは離散化誤差による影響です。この誤差をゼロにするのが理想ですが、現状では誤差をゼロにできないので、いかに誤差を小さくするかが勝負になります。

逆に誤差を小さくしようとすると計算の不安定性が現れます。これは実際の例を見てもらえるとわかりやすいと思うので、次回の中心差分で解説しましょう。簡単に説明すると、矩形波のように波形状が大きく変化する流れだと、時間とともに誤差が増大して発散してしまう現象です。

それでは、これらの原因となる離散化について解説します。

非定常項と移流項の離散化

ナビエ・ストークス方程式は連続的な式なので、離散化を行う必要があります。まずは非定常項と移流項の離散化について説明します。

微分は傾きというのは、高校生のときに習ったと思いますが、離散化は微分に幅をあたえてやる作業です。点を線で表現するので、当然誤差は出てきます。

非定常項でいうと下記のように離散化できます。

$$\frac{\partial v}{\partial t}\approx \frac{v(t+\Delta t)-v(t)}{\Delta t} $$

右辺の分子は速度vの時間変化、分母は時間幅を表しています。この式は両辺が成り立っているわけではなく、離散化による誤差が出てきています。今回は、最も使用される時間一次で離散化したので、１次誤差が出てきます。

このように連続的な式を離散化すると、その過程で誤差が出てきます。誤差は非現実的な計算結果を引き起こす原因になりますので、誤差を抑える手法を取り入れると制度がどんどん上がっていきます。

次は移流項の離散化について解説します。

先述した移流方程式の誤差と不安定性は、主に移流項の離散化が原因です。移流項は格子法においては最も離散化が難しいため、多くの離散化手法があります。今回は代表的な中心差分を紹介します。

$$ c \frac{\partial v}{\partial x} \approx c \frac{v_{i+1}-v_{i-1}}{2\Delta x} $$

離散化すると誤差が発生するので、完全にイコールの式にはなっていません。中心差分では、分子は速度ｖに関して節点iの両端のi+1とi-1、分子は格子幅の２倍となっています。

両端の節点を使っているというのがポイントで、このような参照の仕方をすることで理論的な誤差を抑えられます。ただし一方で、計算が不安定になり、急激に数値振動が増大するようになります。実際に計算した結果は下記のようになります。右に流れる矩形波を一定時間毎にプロットしていますが、動いてすぐに振動が増大していることが分かります。

なぜこのようなことが起こるのかというと、両端を参照するということは一つ飛びで参照する形になります。その結果、間のi点での変化が無視される形になり、正確な結果から離れるせいで不安定性を発生します。詳細な説明は省きますが、急激な変化点の部分だけでも手計算してみると誤差が増大していく現象が確認できると思います。