物理シミュレーションでは連続的な値を扱えないため、微分がある場合は離散化が必要となります。
離散化は空間と時間どちらに対しても必要であり、今回説明するルンゲクッタ法は時間方向の離散化を行うものです。
通常、物理シミュレーションの時間進行はある時点での値($v^n$)に対して、変化量($a \Delta t$)を与えて更新を行います。
ルンゲクッタ法では、この変化量を工夫して取得することで、高次精度を実現します。
ルンゲクッタ法は他の手法に比べて、メモリ使用量を抑えてかつ手軽に高精度化できます。よく使われる手法なので、理解しておくと便利です。
ここでは1段1次(オイラー法)、2段2次、4段4次のルンゲクッタ法について説明します。
1段1次のルンゲクッタ法(オイラー法)
1段1次のルンゲクッタ法は、陽的オイラー法を指します。
ここでは下記の式を用いてオイラー法を説明します。
$$ \frac{dx}{dt} = f(t) $$
$f$は$t$の関数であり、$x$が時間$t$で時々刻々と変化するとします。
その場合、次のステップ$x^{n+1}$を求めたい場合はオイラー法では下記のように書きます。
$$ x^{n+1} = x^n + f(t) \Delta t + O(\Delta t^2)$$
最後の項が誤差の次数を表す項であり、オイラー法では2次の誤差がでるため1次精度となります。
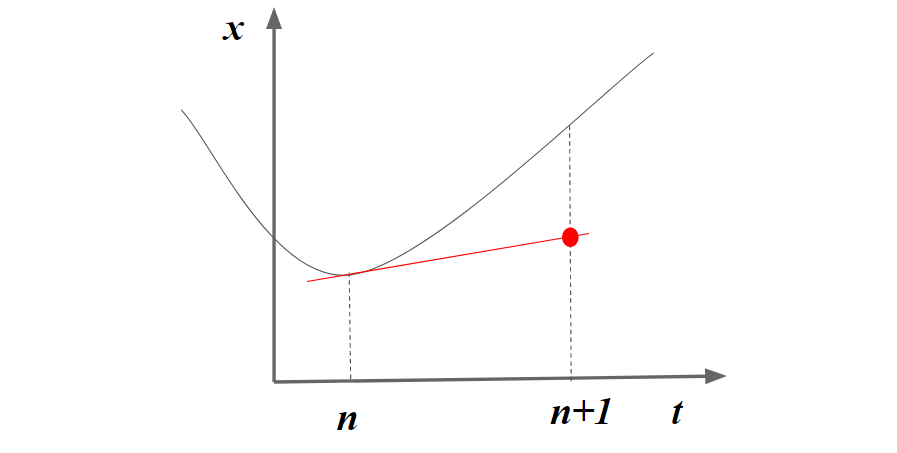
直感的に考えると1段1次のルンゲクッタ法では、下記のようにnステップの位置の傾きを利用します。下記を見るとわかるように、ステップの幅が大きくなると大きな誤差が発生する原因となります。
2段2次のルンゲクッタ法
2段2次では下記のように表せます。
$$k_1 = \Delta t f(x^n, t^n)$$
$$ x^{n+1} = x^n + \Delta t f(x^n + \frac{1}{2}k_1, t^n + \frac{1}{2} \Delta t) + O(\Delta t^3) $$
ここで$k_1$ はルンゲクッタ法で使われれる中間変数です。
このようにルンゲクッタ法では中間ステップをはさむことで高精度します。
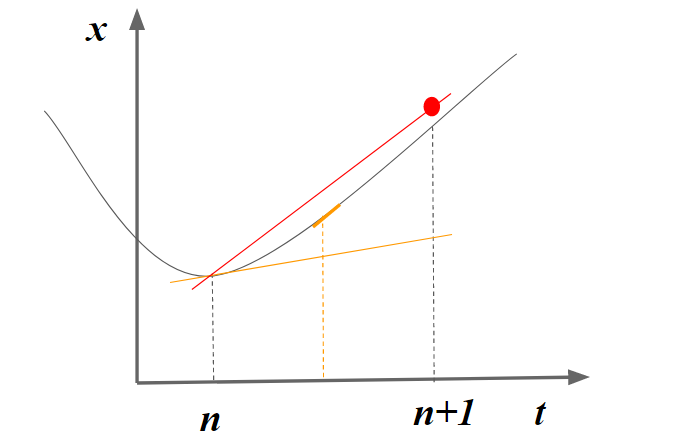
直感的に考えると2段2次のルンゲクッタ法では、下記のように中間の位置の傾きを利用するため、高精度となることがわかります。
4段4次のルンゲクッタ法
さらに高次にしていくと4次のルンゲクッタ法ができます。
$$ k_1 = \Delta t f(x^n, t^n)$$
$$ k_2 = \Delta t f(x^n + \frac{1}{2} k_1, t^n + \frac{1}{2} \Delta t ) $$
$$ k_3 = \Delta t f(x^n + \frac{1}{2} k_2, t^n + \frac{1}{2} \Delta t ) $$
$$ k_4 = \Delta t f(x^n + k_3, t^n + \Delta t)$$
$$ x^{n+1} = x^n + \Delta t (\frac{1}{6} k_1 + \frac{1}{3} k_2 + \frac{1}{3} k_3 + \frac{1}{6} k_4) +O(\Delta t^5)$$
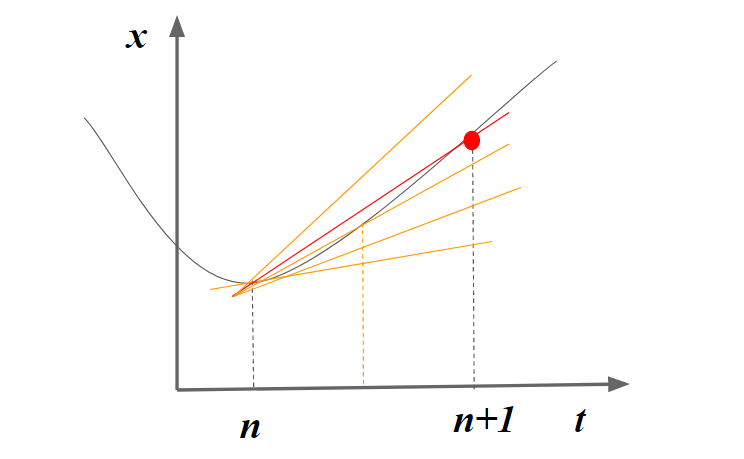
ルンゲクッタ法では4回の修正が行われるため、その分だけ高精度となります。
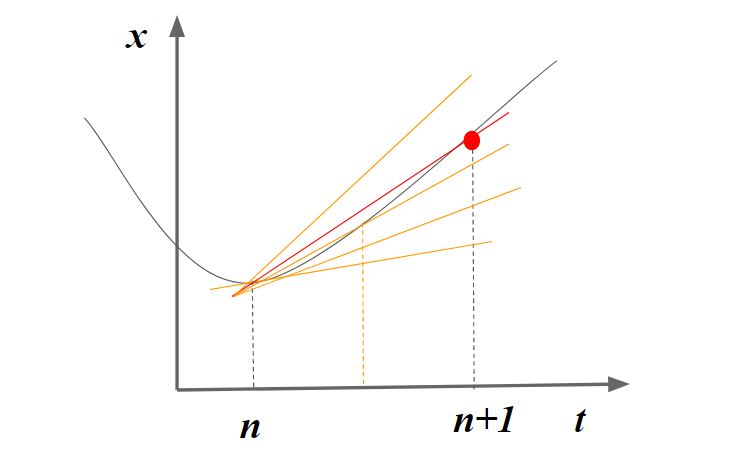
次数の選び方
ルンゲクッタ法では効率の良さの観点から、4段4次がよく利用されます。
これは、5段にしても4次精度、6段にして5次精度であるように、5段以上すると計算量のわりに精度が上がらないためです。
よって、精度が高いほど嬉しい場合は4段のルンゲクッタ法を使用し、さほど精度を求めてない場合は2段のルンゲクッタ法を使うと良いでしょう。
おわりに
今回はルンゲクッタ法について説明しました。
ルンゲクッタ法は1回のステップで多段計算を行う手法であり、他にも時間離散化の手法はあります。
例えば、過去の時間ステップの情報を用いる予測子・修正子法などがあります。
他の手法に比べてルンゲクッタ法が優れているのは、メモリ使用量の少なさにあります。
1ステップ内の情報のみで計算が完結するため、他のステップの情報を保存する必要がありません。
例えば予測子・修正子法で高精度を得ようとすると、過去の数ステップ分の情報を全て保存しておく必要があり、メモリ使用量が数倍になることもあります。
これは、元々のデータ量が少なければ気になりませんが、例えば大規模計算などであればメモリ使用量が数倍になることでメモリ不足を引き起こす原因となります。
よって、数値シミュレーションなどの大規模計算で高精度を得たい場合は、ルンゲクッタ法が最善の選択肢となるでしょう。
 ITとCFD入門サイト
ITとCFD入門サイト