【CFD/格子法】odd-even-SOR（red-black-SOR）法とは？

今回は、red-black-SOR法について説明します。

odd-even-SOR法は別名red-black-SOR法やChebyshevSOR法（おそらくこれが正しい）とも呼ばれます。

一言でいうと、並列性を向上させた行列ソルバーです。

SOR法

まず前提知識として、SOR法（Successive Over-Relaxation method）について説明します。

SOR法とは、ガウスザイデル法というソルバーをもとにしており、ガウスザイデル法はヤコビの反復法をもとにしているので、下記のような順でカスタマイズが進んでいます。

ヤコビの反復　→　ガウスザイデル　→　SOR法

そのため、ざっくりと全部について説明します。ここでは流体解析の圧力計算として使用される「ポアソン式」を例に扱います。

ヤコビの反復法

ヤコビの反復法では、「古いステップⁿの値のみを用いて新しいステップⁿ⁺¹を計算」します。ポアソン式でいうと下記のようになります。

式自体は大して重要ではないので、中身を理解する必要はありません。重要なのは、上付きの添字です。

上付き添字は時間ステップを表しており、上の式では左辺にある$p^{n+1}$という未来の時間ステップの値を右辺の$p^n$という現在の時間ステップの値で表現しているところです。

これがヤコビの反復法の考え方です。図で表すと下記のようになります。

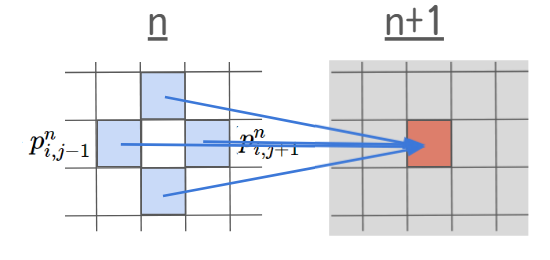
n+1の時間ステップの値を計算するのに、nの時間ステップの値を使用していることがわかります。

ガウスザイデル法

ヤコビの反復法には大きな欠点があり、それは式が成り立っていないことです。ヤコビの反復法で示した下記の四季ですが、時間ステップが左右で違っているのでイコールにはなりません。厳密にはニアリーイコール（ほぼ同等）です。

だからといって、全てを未来のステップの参照にしたら、そもそも計算すらできなくなってしまいます。そこで、未来のステップを少しでも多く混ぜることで厳密な解に近づけようとしたのがガウスザイデル法です。

ガウスザイデル法は、ヤコビの反復法に対して「新しいステップⁿ⁺¹の値も使用する」方法です。それにより、収束性が良く、さらにデータを上書きできるのでメモリ効率も良いという特徴があります。

ポアソン式としては、下記のようになります。

ヤコビの反復法の違いとしては、右辺のpの一部が$p^{n+1}$になっていることです。

これは、格子の並びによってnとn+1のどちらを使用するかを決めているためです。格子点に沿って順に計算していくと、周囲の点の半分は既に計算した値となります。つまり、ポアソン式で参照している計算点の半分はn+1の時間ステップを使用できるということです。

図で示すと下記のようになります。例えば、左上から順に計算していくと、左と上の点はn+1のステップの値を使用できますが、右と下の点はnステップの値を使用することになります。

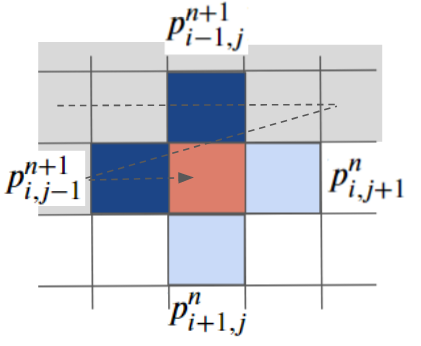
ガウスザイデル法の強みは収束性の向上だけではありません。ガウスザイデル法はメモリ効率も良いです。

ヤコビの反復法では、nステップの値とn+1ステップの値を全てメモリに保存しておく必要がありました。しかしガウスザイデル法は、nの値をn+1で更新していくことができるため、理論上はメモリの使用量が1/2になります。

これはCFDのような大規模計算では非常に重要なことです。メモリの制限で計算サイズが決まってしまうこともあるCFDでは、どのようにメモリを節約するかを検討するだけでも成果につながることが少なくありません。

最近はメモリも安くなりましたが、それでもメモリ使用量を下げることには意味があります。メモリ使用量が下がれば、CPUのキャッシュを有効活用できるようになるので、メインメモリよりも高速なアクセスが可能になります。つまり簡単に言うと、メモリを節約できれば計算が速くなるということです。

SOR法

前置きが長くなりましたが、メインのSOR法について説明します。

SOR法は Successive Over-Relaxation method の略称で、「重み係数ｗを用いることで収束性をコントロールする手法」です。

SOR法では重み係数がキーとなり、パラメータ調整によって強制的に収束性を高めるという泥臭い手法です。経験的にどれくらいのパラメータで収束性が上がるのかは先行研究で判明しているので、それを当てはめるだけでOKです。

SOR法では下記の式を使います。

大きく違うのは、右辺第一項目が追加されたことと第二項に重み係数wがかかっていることです。

これはつまり、n時間ステップの値に対してポアソン式の計算結果をどのくらいブレンドするかを重み係数で決定することを意味しています。w=0だと全く更新されず、w=1だとガウスザイデル法と同じ結果になります。

SOR法では、この重み係数wに対してw>1の値を代入することで、過緩和を発生させます。これにより、強制的にポアソン方程式の収束性を高めることができます。

過緩和は当然ですが計算の安定性を低下させます。そのため、大きくすればよいという話ではなく、安定と収束のバランスを取ったところを指定するというのが基本です。過去の研究から1.5~1.6が取られることが多いと思います。

odd-even-SOR（red-black-SOR）法

とうとう本題の odd-even-SOR 法について説明します。

odd-even-SOR法は別名red-black-SOR法やChebyshevSOR法（おそらくこれが正しい）とも呼ばれます。以下では odd-even-SOR法と呼ぶこととします。

SOR法の弱点として、順番にアクセスするという前提があり、並列性に向かないという問題があります。

例えば下記でいうと、赤いセルの計算前に青のセルの計算は必ず終わっていないといけません。そのため、SOR法は計算の順番が重要な手法であると言えます。（厳密には”ガウスザイデル法”が計算の順番が重要な手法です）

これは並列計算とは非常に相性が悪いです。CFDを並列計算する場合、多数のCPU内のコアを使用することで格子点を手分けして計算します。しかし、SOR法では順番を重視すつため、他のコアの計算の進捗によってコアの身動きが取れないということになりえます。

そのため、SOR法は並列性に問題があります。

そこで、SOR法の並列性を特化した手法として、 odd-even-SOR法が考案されました。

odd-even-SOR法

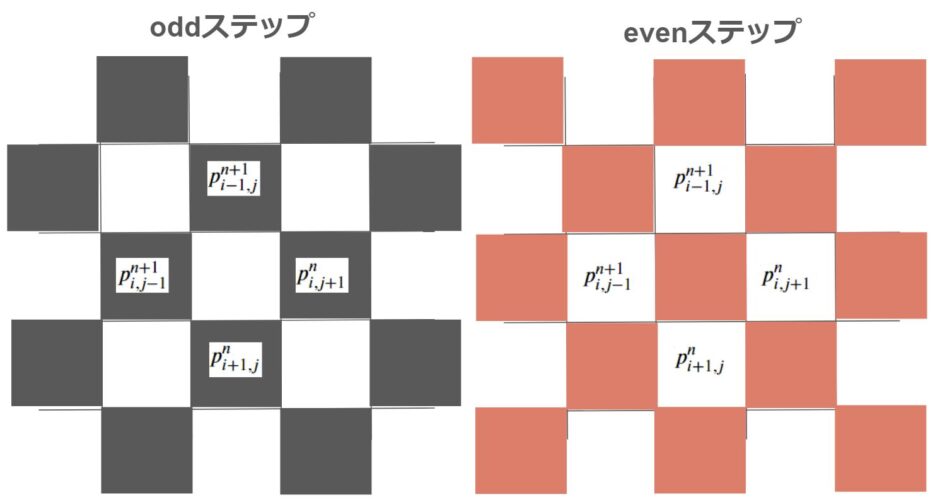
二次元格子のポアソン式を考えましょう。x方向をiとして、y方向をjとしたときに奇数となる計算点をodd、偶数となる計算点をevenと呼びます。

ポアソン式では、oddの点を計算するためにはevenの点を参照します。一方で、 evenの点を計算するためにはoddの点を参照します。

この２つのステップを順番に計算していくのが、odd-even-SOR法です。

図で表すと下記のようになります。

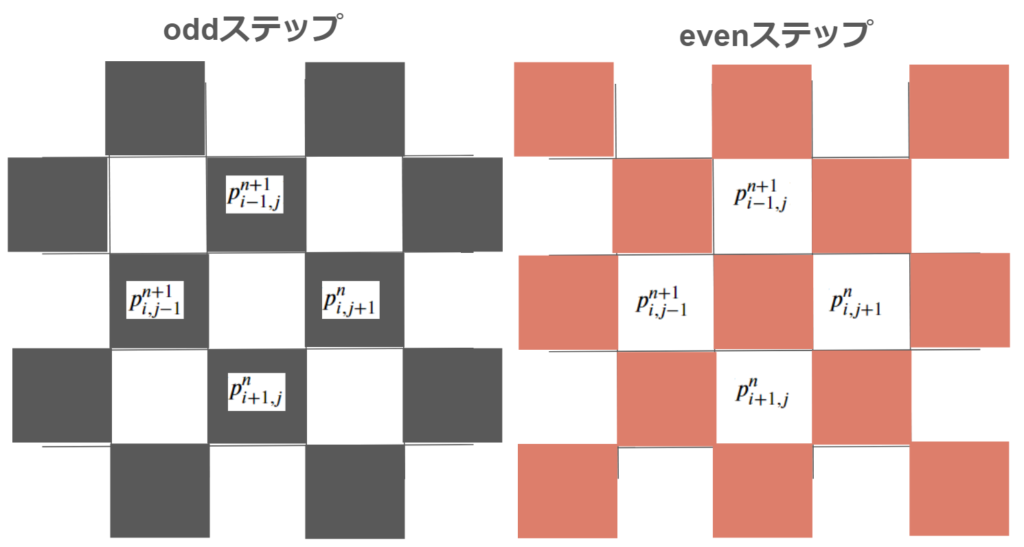
周囲の値を使って、黒を計算　→　赤を計算　→　黒を計算 … というように順番に計算していくことになります。このように赤黒で表すこともあるのでred-black-SOR法と呼ばれることもあります。意味は一緒です。

もちろん、odd点だけを計算するというステップと even点だけを計算するというステップに分かれるために、SOR法と計算は大きく異なります。ただ、それを加味しても並列性の向上によるメリットが大きいため、odd-even-SOR法は使用されることになります。

並列性の向上

SOR法では計算の順番が非常に重要でしたが、odd-even-SOR法にすることでかなり並列性が改善されます。

odd-even-SOR法は下記のような手順となるため、各ステップにおいて格子点間の依存関係が全くありません。これはodd点ではeven点しか参照として使用しないので、odd点同士では参照しないからです。even点でも同様です。

odd点の計算　→　 even点の計算　→ odd点の計算　..

SOR法と比べると違和感はあるかもしれません。ただ、ポアソン式の並列性向上はCFDにおいて大きな課題であるため、多少泥臭い方法であっても使いたいというのが本音です。

シングルスレッドコアの計算性能は１０年以上停滞している現代では、並列性能＝計算性能です。そのため、並列計算に特化した手法というのは成果に直結します。

そのため、odd-even-SOR法は注目に値する手法であるといえます。

おわりに

今回はodd-even-SOR法について説明しました。

他にもCFDやプログラミングに関する初心者向け講座を作成しているので、御覧ください。

youtubeもやっているのでどうぞ。