【CFD/格子法】保存性・有界性・輸送性

今回は保存性・有界性・輸送性について説明します。

かなり短いメモ的な内容ですが、理解の助けになれば幸いです。

保存性

保存性とは、「共通の界面を通過する流速は等しくないといけない」という特性です。

例えば、下記のような図を考えてみましょう。

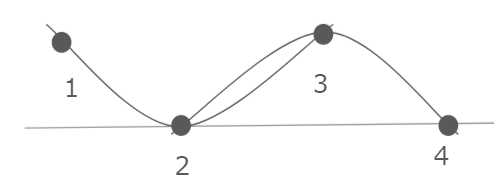
上の図では、各格子点に対して二次補間を行っています。二次補間は精度が上がりますが、保存性が一つの障害となります。

上記の図でいえば、単純に二次補間を行うだけでは二つの補間の間に整合性が取れないという問題が発生します。２番の格子点と３番の格子点の間で値が一致していないため、どちらの補間値を使用するかで流速が異なる結果となってしまいます。

だからといって二次補間を使ってはいけないというわけではなく、保存性を満たすスキームを使えば問題ありません。QUICK法など整合性のとれたスキームを使用するのが望ましいです。

有界性とは、「反復法が収束する十分条件」です。

「対角優位」という条件を満たすことで、収束性が向上します。対角優位とは、行列計算における対角成分が非対角成分に比べて大きいという条件です。有界性を満たす上で望ましい性質です。

有界性は、生成項がない場合は境界値で決まります。

有界性を満たさない場合は、数値振動により収束しないことがあります。

輸送性は対流と対流の相対的な強さであり、ペクレ数で表されます。

$$ Pe = \frac{F}{D} = \frac{\rho u}{\Gamma / \delta x} $$

Fは対流、Dは粘性を表します。$\rho$は密度、uは流速、$\Gamma$は粘性係数、$\delta x$は代表長さを表します。

拡散だけの場合は、$Pe = 0$となり、周囲の計算点の影響を受けます。

移流だけの場合は、$Pe = \infty$となり、片方（上流側）の影響を受けます。

輸送性は、移流などの離散化スキームを決定する上で重要な項目になります。

今回は、保存性と有界性、輸送性について説明しました。

それぞれCFDを学ぶ上で避けて通れない性質です。ぜひ理解しておきましょう。

CFDに関する解説動画も出しています。よかったらどうぞ。