【粒子法】分子動力学法（MD）とは

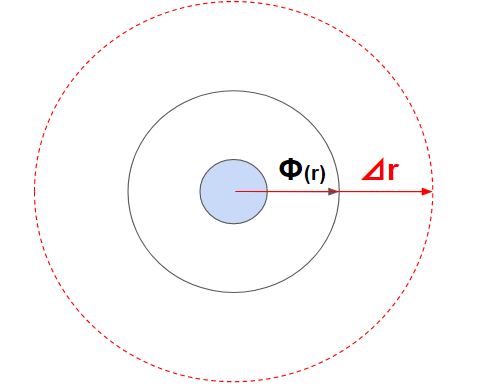
分子動力学法（MD:Molecular Dynamics）とは、原子の運動を見ることで各原子の引力・斥力による相互作用を見る解析です。

（原子動力学法ではなく分子動力学法である理由は歴史背景によるものであり、実際は原子を扱います）

ここでいう引力・斥力とは、原子間のポテンシャル力を意味します。原子同士には力が働いており、個々の原子に対してポテンシャル力計算することで化学反応を計算機上で再現することができます。

膨大な原子に対して長時間の計算が必要であり、分子動力学には大規模なコンピュータが使用されます。

膨大かつ長時間の計算が必要な理由としては、原子のスケールの小ささにあります。空間的にも分子スケールであり、時間も$10^{-15}$程度と非常に短いです。そのため、我々が観察したいスケールの現象を見るためには大規模かつ長時間の計算が必要になってきます。

分子動力学の基本

分子動力学はポテンシャル力による周囲の粒子との相互作用を計算するだけで結果が得られます。

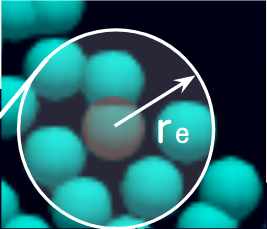
ここで、ポテンシャル力は周囲の粒子との近さで決まります。半径距離$r_{ij}$に応じた重み関数$\phi$を計算し、その総和の微分を取ることで粒子にかかるポテンシャル力$F$が計算できます。

$$ E_i = \sum \phi (r_{ij}) $$

$$ F_i = – \frac{\partial E}{\partial r_i} $$

このポテンシャル力はグラフで表すと下記のようになります。

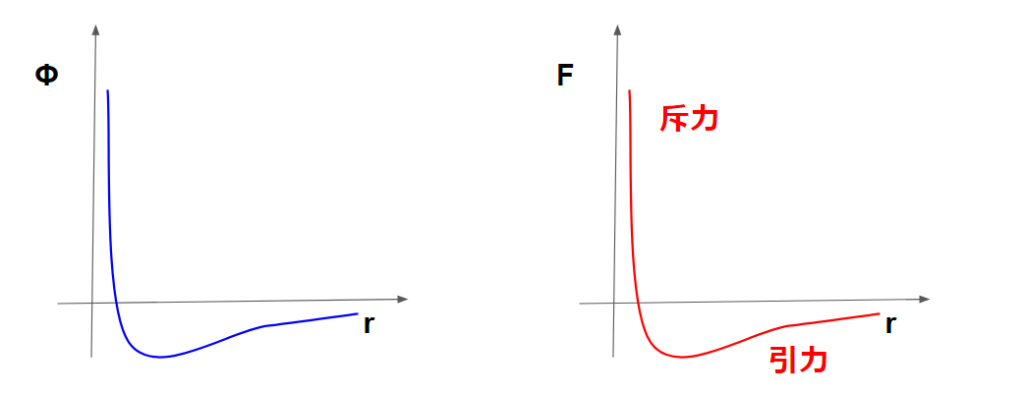
これはつまり、近すぎると反発し遠すぎると引き合うという関係を表しています。

ポテンシャル力により計算結果が大きく変わるため、関数は複数あります。例えばざっくりと下記のようなものがあります。

分子動力学において計算高速化は非常に重要な課題です。

スパコンの利用率として多くを占めるほどに分子動力学は計算リソースを必要とします。単純に計算リソースを投下しても良いですが、まずやるべきはアルゴリズムの最適化です。

ここでは簡単な高速化としてセルインデックス法について説明します。

まず、分子動力学法で最も計算時間のかかる部分は粒子探索です。大量の粒子があって全ての粒子に対して２粒子間の相互作用の判定を行う場合、粒子数Nに対してN(N-1)/2回のループ計算が必要となります。

N(N-1)/2回は粒子数に対して２乗の速度で計算量が増加するため、大規模計算に不利になります。

そこで、近傍粒子探索手法を取り入れます。近傍粒子探索手法は、遠方にある粒子との判定が無駄なので省くということを行います。

一番簡単なのが、一回り大きな円を作ってその部分にある粒子とだけ判定するというものです。

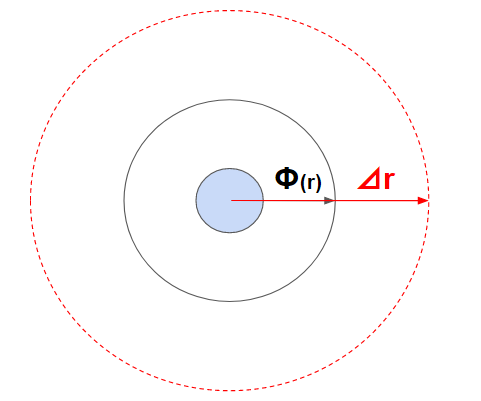
これをブックキーピング（短距離相互作用）と呼びます。広めの範囲は毎ステップ更新するわけではなく、粒子の速度に合わせて最低限更新することで計算量を低下させます。

これをもっと便利にしたのがセルインデックス法です。

セルインデックス法では、まず粒子の座標データからどのセルに含まれるかを調べます。そして、その隣り合ったセルに所属する粒子だけを近傍粒子として判定する手法です。

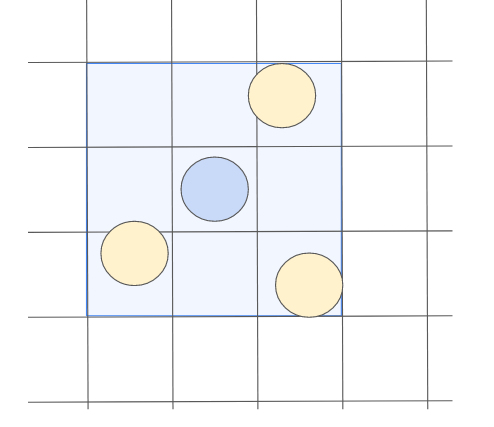
この手法は分子動力学法だけでなく、他の流体解析で使われる粒子にも活用されており、最もポピュラーな手法となっています。

今回は分子動力学法について説明しました。

分子動力学法（MD）は、非常にシンプルですが使用者が多く計算の専門家以外にも化学の専門家に多く使われる手法です。

また分子動力学法をもとに流体解析の粒子法（SPH,MPH）なども派生していることから、多岐に渡る分野に関わる手法とも言えます。まずは基本を抑えて他の手法に応用していくと良いでしょう。

他にも粒子法の解説をしているので、よければこちらもどうぞ。

【CFD/粒子法】格子法と粒子法の違い　【粒子法入門　#1】