【CFD/格子法】レベルセット法（LevelSet法）について解説【格子法入門 #9】

レベルセット法は、領域を２つに分ける解析手法です。流体解析、画像分析やトポロジー解析といった分野で使われています。レベルセット法の大きな利点として、２つの領域の界面を鮮明に捉えられるという特徴があります。

今回は、そのレベルセット法についてできる限りわかりやすく説明したいと思います。

前回は混相流モデル3種（VOF法・レベルセット法・フェーズフィールド法）の概要について解説しました。下記からどうぞ。

【CFD/格子法】混相流モデル（VOF法、Level Set法、フェーズフィールド法）　【格子法入門 #8】

今回は、その一つであるレベルセット法について詳しく説明します。

レベルセット法とは？

レベルセット法（Level Set Method）は、境界を判別するための手法です。一つ次元を上げることで、柔軟に境界の変化を捉えることができます。

例えば、二次元の２つの境界を分ける場合を考えましょう。この場合、レベルセット法では３次元の境界を考えます。この境界において$\phi = 0$となるレベルセット関数を考えます。レベルセット関数は境界を０として片側には大きく、片側には小さくなっているので、下記のように表されます。

$$ \phi > 0 　@領域の内側$$
$$ \phi = 0 　@境界$$
$$ \phi < 0 　@領域の外側$$

図で表すと下記のようになります。青い面より上にあるのが、$\phi > 0$の範囲で、青い面より下にあるのが$ \phi < 0$の範囲です。

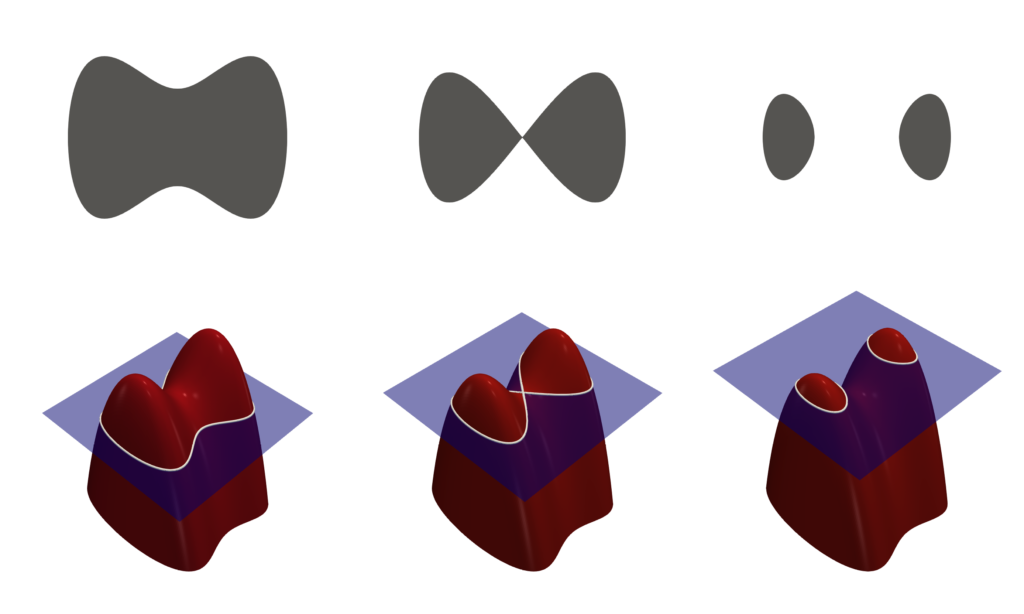
図で表すとわかりやすいですが、レベルセット法の一番のメリットは境界が２つに分かれられることです。これは、２次元空間に対して、３次元で表した恩恵です。２次元に対して、２次元の手法を使用すると、このような境界の分裂は表現できません。

それでは、実際の式を見てみましょう。

$$ \frac{\partial \phi}{\partial t} = v \nabla \phi = 0$$

$t$は時間、$v$は速度です。$\phi$は前述の通りレベルセット関数です。つまり、これは流体解析でいう、移流方程式と同じです。余談ですが、流体解析ではVOF法というものも代表的であり、こちらもレベルセット法と同様に、領域を表す変数を移流方程式で運ぶような手法となっております。

ただし、レベルセット法では一般的に境界の法線速度$F$を使用したハミルトンヤコビ式で表されます。

$$ \frac{\partial \phi}{\partial t} = F |\nabla \phi | = 0$$

ここで、$F$は境界の法線速度$F = n \cdot \frac{dx}{dt}$を表し、$n$は法線ベクトル$n = \frac{\nabla \phi}{| \nabla \phi|}$を表します。この式を時刻が進むごとに解くことで、徐々に境界が変化する様子を観察します。

レベルセット法には、再初期化という手順があります。これは、レベルセット法が境界を鮮明に捉えるために、重要な手順です。

移流方程式を解こうとすると、必ず拡散が起こり、値がぼやけます。これは、レベルセット法も同じです。そのため、界面を鮮明に捉えるためには、界面を強制的に圧縮してやる必要があります。そのための手順が最初期化です。

レベルセット法では、下記の式を満たすことをルールとしています。これは、境界において、レベルセット関数の傾きが1になることを表した式です。

$$ |\nabla \phi | = 0　@\phi = 1$$

しかし、先述したように、計算を進めると徐々にこれを満たさなくなります。そのため、再初期化を行います。最初期化は、以下の式で行います。

$$ \frac{\partial \phi}{\partial t} = sign(\phi) (1 – |\nabla \phi|)$$

ここで、$sign(\phi)$は符号を表す関数で、$sign(\phi) = \frac{\phi}{\sqrt{\phi^2+\epsilon^2}}$を表します。$\epsilon$はゼロ割を防ぐための微小値です。

以上の手順により、境界の移動と最初期化を繰り返して、レベルセット法使用した境界探索を解くことができます。境界の移動の式に関しては、流体解析だと速度値がありますが、画像分析だとエネルギーの最小化式によって解くみたいです。

今回は、レベルセット法（Level Set Method）について解説しました。

レベルセット法に関して、重要なポイントは下記の通りです。

レベルセット法は色々と派生した手法も多く、特に流体解析の分野ではCLSVOF法と呼ばれるVOF方とレベルセット法を組み合わせた手法も有名です。境界の鮮明化は重要な技術なので、覚えておいて損はないでしょう。

youtubeで色々な解説動画を出してます。どうぞ。