【LBM】計算フローとプログラミング【格子ボルツマン法講座 #8】

はじめて格子ボルツマン法を学ぶ初心者のための講座、第８回になります。

格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。

全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD（流体解析）の手法を知っておくとベターです。

前回は格子ボルツマン方程式の境界条件として壁面・流入流出・周期境界について説明しました。下記からどうぞ。

【LBM】境界条件（バウンスバックなど）【格子ボルツマン法講座 #7】

重要なポイントは下記のとおりです。

壁面は一般的にバウンスバックが使われる
バウンスバックは分布関数が来た方向に跳ね返るというモデルである
バウンスバックは壁面で流速をゼロとする
バウンスバックは大きくハーフウェイとオングリッドの２つに分けられる
フリースリップモデルを使えば、滑る壁面を扱える
動く壁の条件を与えることで、壁の接線・法線方向に速度を与えられる
流入条件には、平衡分布を直接与えることもできる
流出条件は、隣の分布関数をコピーする
周期境界条件は、両端の壁がつながっている状態で、並進ステップの拡張で表現できる

今回はプログラミング例を入れながら計算フローについて説明していきたいと思います。動作検証はしていないため、プログラミングのイメージをつかむための参考程度にしてください。

計算フローとプログラミング

今までの回で一通り理論については説明したため、ここからはプログラミングの例も入れつつ具体例を出していきましょう。

格子ボルツマン法の計算フローは下記の流れになります。

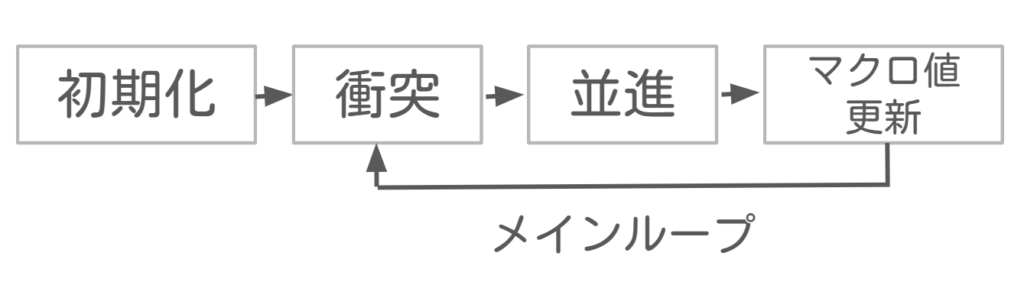
この手順に沿って、どんな式を使ってどんなプログラムを書けばよいのかを具体例に触れつつ学んでいきましょう。

初期化

初期化のステップにおいて設定すべきなのは、マクロ量と分布関数$f$です。

マクロ量はシンプルに考えるため、初期値は流速$u_x = 0 $、$u_y = 0 $ で密度 $ \rho = 1$ とします。これらは無次元量なので、計算が安定する範囲内であれば好きな値にして大丈夫です。

分布関数$f$の初期値としては、平衡分布関数$ f^{eq} $を与えるのが一般的です。

平衡分布関数$f^{eq}$は下記の式で与えられます。

$$ f_i^{eq} (x,t) = w_i \rho (1 + \frac{u \cdot c_i}{c^2_s} + \frac{(u \cdot c_i)^2}{2 c_s^4} – \frac{u \cdot u}{2 c_s^2}) $$

例えば、D2Q9モデルだと下記のように方向を採番します。

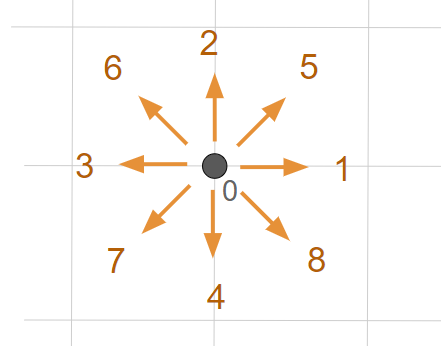
式のイメージがまだ持ちにくいと思うので、$c_i$に具体的な数値を入れた例も出しましょう。

音速を$c_s = \frac{1}{sqrt(3)}$として各方向について計算すると、下記の式が得られます。

$$ f_0^{eq} = \frac{2 \rho}{9} (2 – 3 u^2) $$

$$ f_1^{eq} = \frac{\rho}{18} (2 + 6 u_x + 9 u_x^2 – 3 u^2) $$

$$ f_2^{eq} = \frac{\rho}{18} (2 + 6 u_y + 9 u_y^2 – 3 u^2) $$

$$ f_3^{eq} = \frac{\rho}{18} (2 – 6 u_x + 9 u_x^2 – 3 u^2) $$

$$ f_4^{eq} = \frac{\rho}{18} (2 – 6 u_y + 9 u_y^2 – 3 u^2) $$

$$ f_5^{eq} = \frac{\rho}{36} [(1 + 3 (u_x + u_y) + 9 u_x u_y + 3 u^2) ]$$

$$ f_6^{eq} = \frac{\rho}{36} [(1 – 3 (u_x – u_y) – 9 u_x u_y + 3 u^2) ]$$

$$ f_7^{eq} = \frac{\rho}{36} [(1 – 3 (u_x + u_y) + 9 u_x u_y + 3 u^2) ]$$

$$ f_8^{eq} = \frac{\rho}{36} [(1 + 3 (u_x – u_y) – 9 u_x u_y + 3 u^2) ]$$

ここで、$u$は速度の大きさを表し、$ u = sqrt(u_x u_x + u_y u_y)$です。

次に、緩和係数の初期値も設定します。緩和係数は下記の式により、粘度により決定されます。

$$ \tau = 3 \nu + \frac{1}{2} $$

ここで、無次元化のため$\Delta t = 1$、$c_s = \frac{1}{sqrt(3)}$を代入していることに注意してください。

初期化プログラム

Pythonプログラムだと下記のようになります。あくまでイメージだけなので、そのままでは動作はしませんのでご注意ください。

nu = 0.01
tau = 3.0 * nu + 0.5
U = 0.01
ux = np.zeros(nx,ny)
uy = np.zeros(nx,ny)
rho = np.ones(nx,ny)
f = np.zeros(nx,ny,9)
fn = np.zeros(nx,ny,9)
w = np.array([4/9, 1/9, 1/9, 1/9, 1/9, 1/36, 1/36, 1/36, 1/36])
cx = np.array([0, 1, 0, -1, 0, 1, -1, -1, 1])
cy = np.array([0, 0, 1, 0, -1, 1, 1, -1, -1])
for x in range(nx):      
  for y in range(ny):
    for i in range(9):
      uxy = ux[x,y] * ux[x,y] + uy[x.y] * uy[x.y]
      cu = cx[i] * ux[x,y] + cy[i] * uy[x,y]
      f[x,y,i] = w[i] * rho[x,y] * ( 1.0 + 3.0 * cu + 9.0 / 2.0 * cu * cu -3.0 / 2.0 * uxy)

これで初期化が完了しました。

今回は初期化は最低限で済ませましたが、もし壁などの境界が複雑であれば、壁面でフラグを立てて整理したりします。その場合は、初期化がもう少しボリュームが増えます。

計算ループ

初期化が終わると、メインループに入ります。

メインループ内で、衝突と並進、境界条件を設定します。

ここからの内容は、計算のforループ内に書くと思って読んでください。

for n in range(1000):
  ・・・

上記では、1000ステップだけ時間を進めます。

衝突

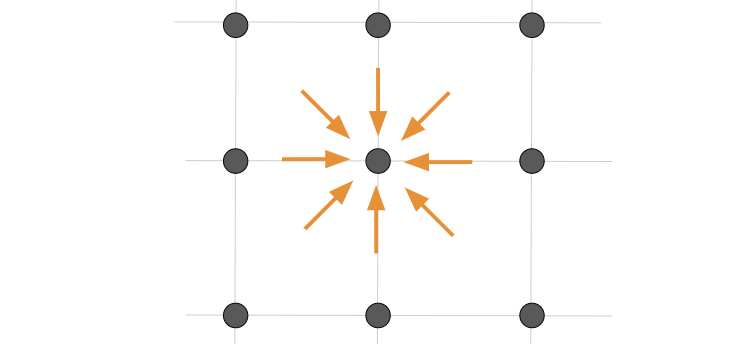
計算ループ内では、まずは衝突を計算します。

格子ボルツマン方程式の衝突ステップのみを取り出した下記の式を実行します。この式は無次元化により、$\Delta t = 1$となっていることに注意です。

$$ f_i^t (x, t) = f_i (x, t) – \frac{1}{\tau} ( f_i (x, t) – f_i^{eq} (x, t) ) $$

分布関数はひとまとめにしたほうが計算量が減るので、下記のように式を変形しましょう。

$$ f_i^t (x, t) = (1 – \frac{1}{\tau})f_i (x, t) + \frac{1}{\tau} f_i^{eq} (x, t) $$

衝突プログラム

Pythonプログラムにすると、下記のようになります。

プログラム上では衝突ステップの一時変数は不要で、分布関数を上書きする形で更新します。

for x in range(nx):
  for y in range(ny):
    for i in range(9):
      uxy = ux[x,y] * ux[x,y] + uy[x.y] * uy[x.y]
      cu = cx[i] * ux[x,y] + cy[i] * uy[x,y]
      f[x,y,i] = (1 – 1 / tau) * f[x,y,i] + w[i] * rho[x,y] * ( 1.0 + 3.0 * cu + 9.0 / 2.0 * cu * cu -3.0 / 2.0 * uxy) / tau

衝突ステップは非常にシンプルに書けることがわかります。

並進

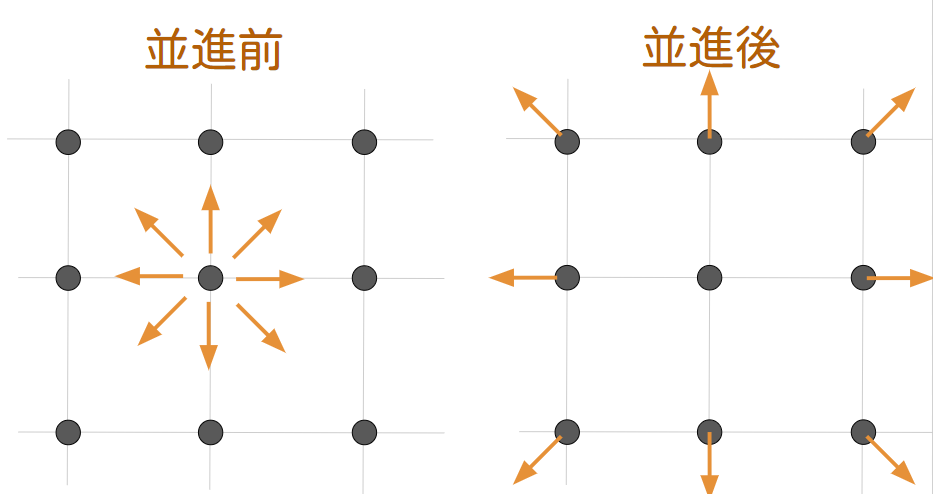
次は並進の計算を行います。

衝突後の分布関数を一時変数$f^t$とすると、並進の計算は下記で行えます。

$$ f_i (x + c \Delta t, t + \Delta t) = f_i^t(x, t) $$

並進プログラム

プログラムだと下記のようになります。並進後の分布関数はfnであることに注意してください。

for x in range(nx):
  for y in range(ny):
    for i in range(9):
      xn = x + cx[i], yn = y + cy[i]
      if xn == nx+1:
        xn = 0
      if xn == -1:
        xn = nx
      if yn == ny+1:
        yn = 0
      if yn == -1:
        yn = ny
      fn[xn, yn, i] = f[x, y, i]

並進ステップでは、隣接セルに粒子が移動します。しかし、両端だと隣接セルが足りないので、例外処理をしないとエラーが発生してしまいます。

そのため、両端では逆の端を参照するようにしており、結果的に周期境界条件が与えられることになります。

境界条件

周期境界条件なら並進ステップまでの処理で問題ないですが、壁などの境界を与えたい場合は境界条件を与える処理を追加しないといけません。

今回はキャビティ流れを想定した境界条件を与えましょう。

キャビティ流れとは、下記のように上面のみに速度を与えた四角形の空間の流れです。流体解析のベンチマークで最もよく使われる例題です。

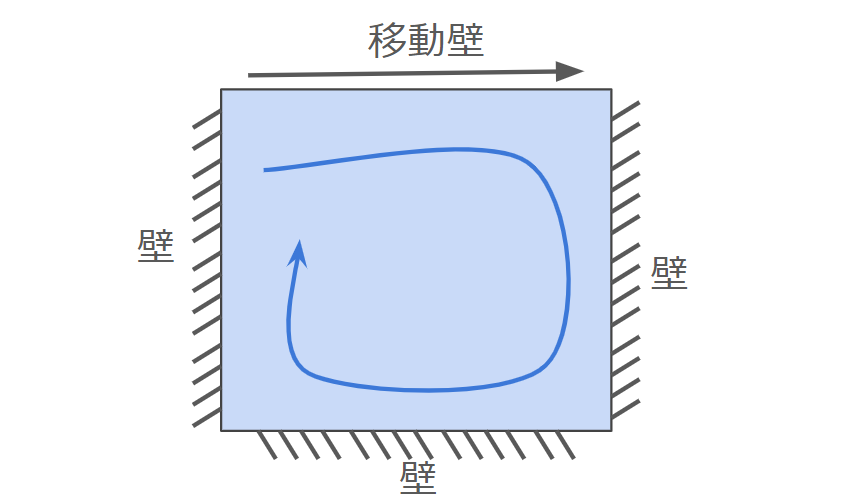
壁面条件としては、ハーフウェイバウンスバックを使用します。

よって、今回はハーフウェイバウンスバックと速度を与える壁の2条件を考えます。

ハーフウェイバウンスバック

ハーフウェイバウンスバックは、下に壁がある場合は下記で計算できます。

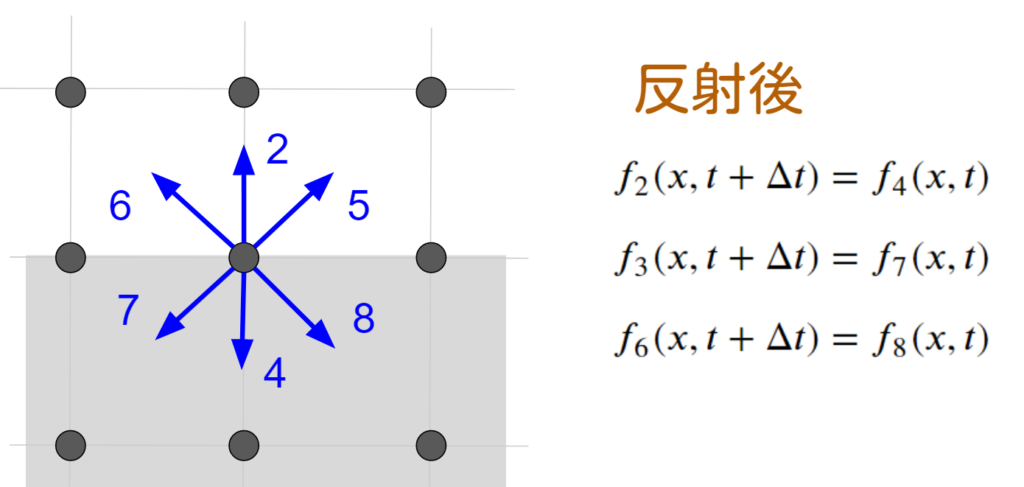
ハーフウェイバウンスバック境界条件の一般式は下記で表されます。

$$ f_{\bar{i}} (x_b , t + \Delta t) = f_i^t (x_b , t) $$

これを左右の壁にも適用します。

上面の動く壁は、ハーフウェイバウンスバックに壁面速度を上乗せした値を返すことで、計算できます。

$$ f_{\bar{i}} (x_b , t + \Delta t) = f_i^t (x_b, t) – 2 w_i \rho \frac{c_i u}{c_s^2} $$

上付きバーは、跳ね返った後の方向を示しています。

ここで注意したいのが、壁面における密度です。

上に動く壁がある場合は、下記の式を用いて密度を計算します。

$$\rho = \frac{(f_0 + f_1 + f_3) + 2 (f_2 + f_5 + f_6)}{1 + V}$$

壁からの分布関数を含まない式で密度が計算されていることがわかります。

ここで、分母の$V$は法線方向速度です。今回は不要なので、$V$はプログラム上では削除しています。

境界条件プログラム

Pythonのプログラムは下記のようになります。

for y in range(ny):
  fn[x, 0, 1] = f[x, 0, 3]
  fn[x, 0, 5] = f[x, 0, 7]
  fn[x, 0, 8] = f[x, 0, 6]
  fn[nx-1, y, 3] = f[nx-1, y, 1]
  fn[nx-1, y, 7] = f[nx-1, y, 5]
  fn[nx-1, y, 6] = f[nx-1, y, 8]
for x in range(nx):
  fn[x, 0, 2] = f[x, 0, 4]
  fn[x, 0, 5] = f[x, 0, 7]
  fn[x, 0, 6] = f[x, 0, 8]
  rho[x, ny-1] = (fn[x, ny-1, 0] + fn[x, ny-1, 1] + fn[x, ny-1, 3] + 2.0*(fn[x, ny-1. 2] + fn[x, ny-1, 5] + fn[x, ny-1, 6]) / (1.0 + 0.0))
  fn[x, ny-1, 4] = f[x, ny-1, 2] – rho[x, ny-1] * (cx[2] * U + cy[2] * 0.0) * 2.0 / 3.0
  fn[x, ny-1, 7] = f[x, ny-1, 5] – rho[x, ny-1] * (cx[5] * U + cy[5] * 0.0) / 6.0
  fn[x, ny-1, 8] = f[x, ny-1, 6] – rho[x, ny-1] * (cx[6] * U + cy[6] * 0.0) / 6.0

マクロ値の更新

並進と衝突の計算を終えたので、マクロ値の更新を行います。

密度と流速は下記で得られます。

$$ \rho = \sum f_i $$

$$ \u = \frac{\Sum c_i f_i }{\rho}$$

マクロ値プログラム

Pythonプログラムだと下記のようになります。

rho[x, y] =fn[x, y, 0] + fn[x, y, 1] + fn[x, y, 2] + fn[x, y, 3] + fn[x, y, 4] + fn[x, y, 5] + fn[x, y, 6] + fn[x, y, 7] + fn[x, y, 8]
ux[x, y] =(fn[x, y, 0] * cx[0] + fn[x, y, 1] * cx[1] + fn[x, y, 2] * cx[2] + fn[x, y, 3] * cx[3] + fn[x, y, 4] * cx[4] + fn[x, y, 5] * cx[5] + fn[x, y, 6] * cx[6] + fn[x, y, 7] * cx[7] + fn[x, y, 8] * cx[8]) / rho[x,y]
uy[x, y] =(fn[x, y, 0] * cy[0] + fn[x, y, 1] * cy[1] + fn[x, y, 2] * cy[2] + fn[x, y, 3] * cy[3] + fn[x, y, 4] * cy[4] + fn[x, y, 5] * cy[5] + fn[x, y, 6] * cy[6] + fn[x, y, 7] * cy[7] + fn[x, y, 8] * cy[8]) / rho[x,y]
for I in range(9):
  f[x, y, i] = fn[x, y, i]

移動後の分布関数$fn$を次のステップの初期分布関数$f$とするために、ループの最後に分布関数の更新を行っています。