はじめて格子ボルツマン法を学ぶ初心者のための講座、第7回になります。
格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。
全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD(流体解析)の手法を知っておくとベターです。
前回は格子ボルツマン方程式からナビエ・ストークス方程式の導出としてChapman-Enskog展開について説明しました。下記からどうぞ。
Chapman-Enskog展開の手順は下記のとおりです。
- 1,摂動展開による主要成分の分解
- 2.主要成分に対してモーメントを計算し、マクロな値にする
- 3.格子ボルツマン方程式から得られたマクロな式と、ナビエ・ストークス方程式が一致するように、変数の値をお設定する
少し多いですが、重要なポイントは下記のとおりです。
- 格子ボルツマン方程式は、ナビエ・ストークス方程式とほぼ同等の結果が得られる
- Chapman-Enskog展開により、ナビエ・ストークス方程式を復元できる
- 摂動展開とは、主要な成分と副次的な成分の分解である
- クヌーセン数とは、分子がどれだけ自由に動けるかを表す指標である
- Chapman-Enskog展開では、摂動展開による主要成分の分解が必要である
- Chapman-Enskog展開では、主要成分に対してモーメントを計算してマクロな値にする
- 格子ボルツマン方程式から導出したマクロな式の変数をナビエ・ストークス方程式と一致させる
前回は格子ボルツマン方程式からナビエ・ストークス方程式が導けることをChapman-Enskog展開を用いて説明をしました。
今回は、また実用的な話に戻って、壁面などの境界条件について説明いたします。
境界条件
格子ボルツマン法は衝突と並進だけの計算であるため、工夫の余地が少ないです。
衝突として、BGKモデル以外にも、特殊な流れまで対応できるMRTやキュムラントモデルなどがありますが、種類は少ないです。
そのため、多くの議論がなされるのが「境界条件」です。ここからは、主要な境界条件について説明していきます。
バウンスバック
バウンスバックは壁面を表す境界として最も使用されます。
バウンスバックは、壁面で衝突した仮想粒子が、来た方向に跳ね返るというモデルです。
図で示すと下記のようになります。
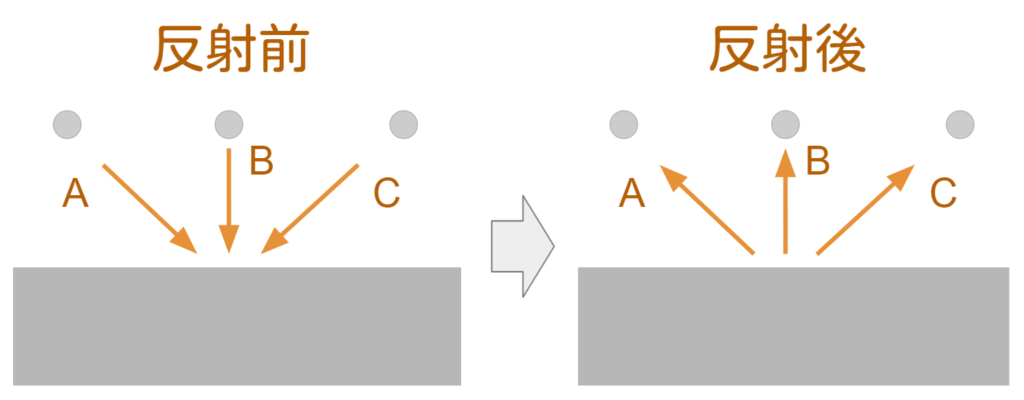
バウンスバック境界条件は下記の式で表されます。
$$ f_{\bar{i}} (x_b , t + \Delta t) = f_i^t (x_b , t) $$
上の式は、衝突後の並進のステップを考えており、$f_i^t $は衝突後の分布関数です。
$x_b$は境界にある計算点を意味しており、上の式は境界だけに適用されます。$f_i$は反射後の方向における分布関数です。
つまり、上の式は$\Delta t$で壁に反射して、来た方向に跳ね返るということを意味しています。
一般化のためにiで表現していますが、イメージしにくいと思うので、実例を見てみましょう。
例えば、番号をふると下記の式になります。
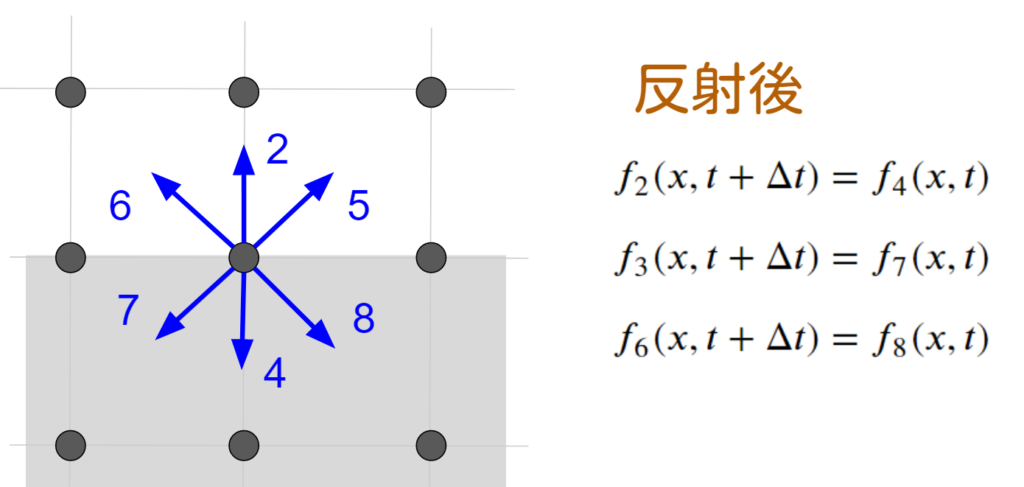
ハーフウェイとオングリッド(フルウェイ)
バウンスバック境界条件は、壁の位置の設定方法によって大きく2つに分けられます。
一つはハーフウェイバウンスバックです。ハーフウェイバウンスバックは、計算点と計算点の間に壁があるモデルです。
もう一つは、オングリッドです。フルウェイとも呼ばれますが、こちらは計算点上に壁があるモデルです。
図で比較すると違いが一目瞭然です。
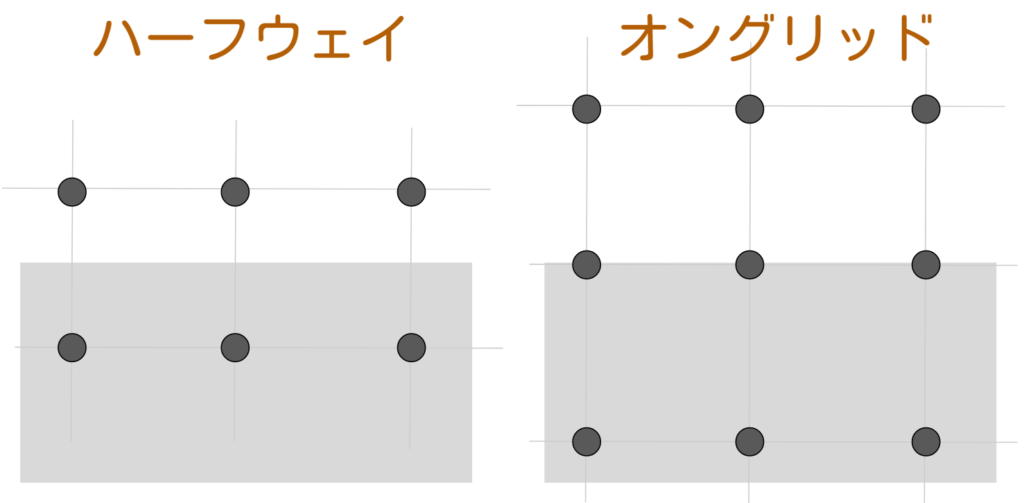
格子ボルツマン法では$\Delta t$で仮想粒子が隣の計算点に移動します。そのため、ハーフウェイでは$\Delta t$で仮想粒子は反射して元の計算点に戻ります。
一方で、オングリッドでは$2 \Delta t$で元の計算点に戻ります。
ハーフウェイが用いられるのが多いと思いますが、2種類あるということは覚えておくと良いでしょう。
フリースリップ
バウンスバック境界条件において、仮想粒子の跳ね返る向きに違和感があるかもしれません。物体で考えると、来た方向にそのまま戻るというのは、イメージと少し異なります。
これは、壁面における流速をゼロにするために来た方向に分布関数を反転されるということが行われています。
壁面に滑りをもたせたモデルはフリースリップモデルと呼ばれ、下記のように動きます。
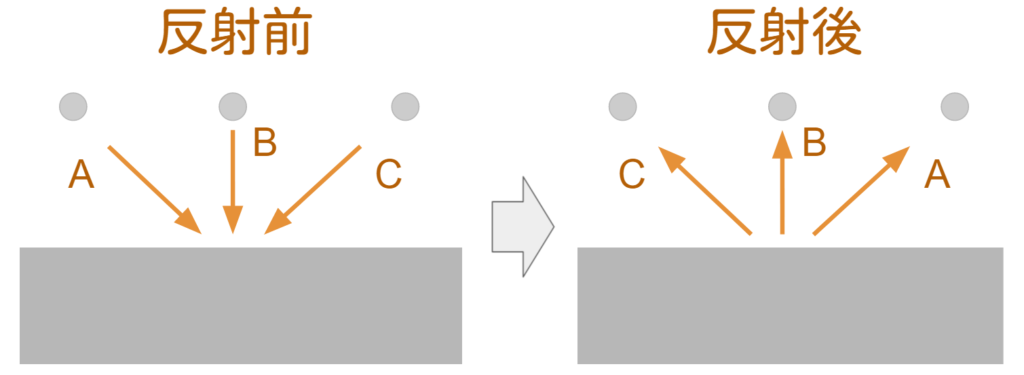
物体の反射とイメージが一致していると思います。つまり、物体の反射は滑りによるで、流体とは少し挙動が違うことがわかります。
動く壁
動く壁の場合は、強制的に壁に速度を与えることになります。
計算としては、跳ね返る前の仮想粒子に壁面速度を上乗せした値を返すことになり、下記の式で表すことができます。
$$ f_{\bar{i}} (x_b , t + \Delta t) = f_i^t (x_b , t) – 2 w_i \rho \frac{c_i u}{ c_s^2} $$
バウンスバックの計算式に対して、右辺第二項にて速度を上乗せしています。
動く壁の速度は接線方向だけでなく法線方向にも与えられます。そのため、流入条件も扱うことができます。
流入・流出
流入条件は動く壁として与えることもできますが、一番簡単なのは平衡分布を直接与えることです。
流入位置の分布関数を下記の平衡分布で上書きすることで、強制的な流れを与えることができます。
$$ f_i^{eq} (x,t) = w_i \rho ( 1 + \frac{u \cdot c_i}{c_s^2} + \frac{ (u \cdot c_i)^2 }{ 2 c_s^4} – \frac{u \cdot u}{ 2 c_s^2}) $$
流出条件についても同様に強制的に流れを与えることができます。
もし圧力出口として与えたい場合は、一般的な格子法と同じように、流出点の隣の分布関数をコピーして与えるということができます。
周期境界条件
次は周期境界条件について説明します。
周期境界は、領域の右端に進むと左端から出てくるように、両端の壁がつながっている境界です。
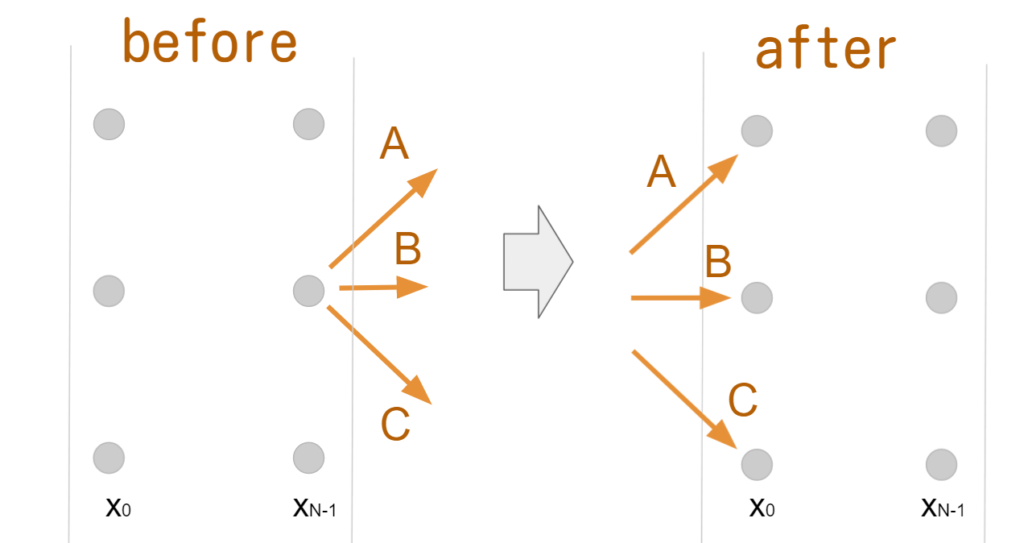
周期境界に入った仮想粒子は、反対の境界から出てくることになります。
計算領域の両端がつながった状態を考えると、並進と全く同じ動きになるため、周期境界は並進ステップとまとめてしまうことが多いです。そのため、わざわざ周期境界条件として別途計算ステップを増やす必要はありません。
周期境界の具体例を下記に示します。

おわりに
今回は境界条件について説明しました。
重要なポイントは下記のとおりです。
- 壁面は一般的にバウンスバックが使われる
- バウンスバックは分布関数が来た方向に跳ね返るというモデルである
- バウンスバックは壁面で流速をゼロとする
- バウンスバックは大きくハーフウェイとオングリッドの2つに分けられる
- フリースリップモデルを使えば、滑る壁面を扱える
- 動く壁の条件を与えることで、壁の接線・法線方向に速度を与えられる
- 流入条件には、平衡分布を直接与えることもできる
- 流出条件は、隣の分布関数をコピーする
- 周期境界条件は、両端の壁がつながっている状態で、並進ステップの拡張で表現できる
必要に応じて適切な境界条件を設定しましょう。
壁面条件は今回は基本のバウンスバックだけを紹介しましたが、他にも種類が多くあります。もう少し難しい壁面条件を使うと、高精度な壁も表現することができます。
さらに、インターポレイテッドバウンスバックなどの更に高度な壁面条件を使うことで、曲面を表現することもできます。また別の機会にて紹介できればと思います。
次回からは、具体的な計算フローとプログラミング例について紹介していきたいと思います。概要は以前説明しましたが、それだけだと実装までイメージできないと思うので、丁寧に具体的な部分まで触れていきたいと思います。
 ITとCFD入門サイト
ITとCFD入門サイト 

