はじめて格子ボルツマン法を学ぶ初心者のための講座、第四回になります。
格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。
全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD(流体解析)の手法を知っておくとベターです。
前回は格子ボルツマン方程式について説明しました。下記からどうぞ。
重要なポイントは下記のとおりです。
- 格子ボルツマン方程式はLBEと呼ばれる
- 分布関数は密度を粒子速度で割った値である
- 分布関数のモーメントを取ることで、マクロな量が得られる
- モーメントとは、粒子速度で積分することである
- フラクショナルステップ法と同様に、LBEも並進と衝突を分けて解く
- 連続的な式を離散化すると、よく見る式になる
- 衝突項が分布関数の時間変化をコントロールする
前回は衝突に関する説明を省略したので、今回は衝突について丁寧に説明したいと思います。
衝突項
格子ボルツマン方程式は下記で表されます。今回扱うのは右辺の衝突項です。
$$ f_i(x + e_i \Delta t, t+\Delta t) – f_i (x,t) = \Omega $$
衝突項$\Omega$は分布関数fの時間変化をコントロールするため、何でも良いわけではありません。流体の保存に関する様々な制約があります。
質量保存
$$ \int \Omega (f) d e^3 = 0 $$
運動量保存
$$ \int e \Omega (f) d e^3 = 0 $$
エネルギー保存
$$ \int |e|^2 \Omega (f) d e^3 = 0 $$
内部エネルギー保存
$$ \int |v|^2 \Omega (f) d e^3 = 0 $$
eは粒子速度、vは相対速度(粒子速度e – 平均速度u)です。
これらの制約を守ったモデルでないといけないため、衝突モデルはまだ多く存在しません。
今回は最も有名な衝突モデルである「BGKモデル」について紹介します。
様々なモデルがありますが、基本的な使い方としては、BGKモデルが非常に簡単であるため、BGKモデルで解析をして問題があった場合に別のモデルを検討するという手順がよく使われます。
BGKモデル(概要)
BGKモデルは最もシンプルな衝突モデルです。
BGKモデルは「一定時間が立つと完全に流れが落ち着く(=平衡状態になる)」という衝突モデルです。
イメージ的には、流体をぐちゃぐちゃにかき混ぜて放置すると、徐々に整流される様子をイメージしてください。これは、マクロ的には粘性や圧力によるエネルギーの損失で説明されますが、格子ボルツマン法では仮想粒子の衝突がエネルギーの損失を発生させます。
BGKモデルは下記の式で表されます。
$$ \Omega (f) = – \frac{\Delta t}{\tau} ( f – f^{eq}) $$
$f^{eq}$は平衡分布関数と呼ばれ、完全に平衡状態となった分布関数を意味します。eqは平衡を意味するequilibriumの略です。
右辺の$f-f^{eq}$は分布関数と平衡分布関数の差分なので、「分布関数の非平衡成分」を意味します。$\tau$は緩和係数であり、非平衡成分(粒子運動の激しさ)に応じて流れが落ち着くことになります。粒子運動の激しさに応じて落ち着き具合が変わるというのは直感的にも正しいと感じるでしょう。
BGKモデルでは、緩和係数$\tau$にスカラー値を設定するため、SRT(Single Relaxation Time : 単緩和時間)モデルと呼ばれます。
他緩和時間モデル(MRT)
BGKモデルがSRTと呼ばれるのに対し、MRT(Multiple Relaxation Time : 多緩和時間)モデルも存在します。
本筋ではないため詳細は省略しますが、MRTモデルの場合は変換行列Mを導入したり、BGKモデルにおける緩和時間$\tau$の代わりに変換行列Mの対角成分を使用したりする必要があります。
MRTはSRTに比べて数値安定性が良いため、高レイノルズ数などの複雑な流れにおいてはMRTでしか計算できない場合があります。
非平衡分布関数$f^{neq}$と平衡分布関数 $f^{eq}$
平衡分布関数$f^{eq}$は、局所平衡分布関数とも呼ばれます。その名の通り、局所的に流れが落ち着いた状態を指します。
ここでいう「落ち着いた状態」が平衡状態を指しており、これは局所的な平衡のことです。マクロ的な流れが完全に静止しているわけではないので、ご注意ください。
非平衡分布関数 $f^{neq}$ は分布関数 $f$ と平衡分布関数 $f^{eq}$ の差分で表されます。
$$ f^{neq} = f – f^{eq} $$
neqは非平衡を意味するnon-equilibriumの略です。
非平衡分布関数を使用すると、衝突項$\Omega$は下記の式で表されます。非平衡分布に比例して衝突が発生することがわかります。
$$ \Omega (f) = – \frac{\Delta t}{\tau} f^{neq} = – \frac{\Delta t}{\tau} ( f – f^{eq} ) $$
衝突項は質量保存を満たすため、下記の式が成立します。
$$ \int \Omega (f) d e^3 = 0 $$
これを用いて衝突項の中を展開すると、下記の式が得られます。
$$ – \frac{\Delta t}{\tau} \int ( f – f^{eq} ) de^3 = – \frac{\Delta t}{\tau} { \int f de^3 – \int f^{eq} de^3 } = – \frac{\Delta t}{\tau} (\rho – \rho ) = 0 $$
つまり、粒子速度で積分すると非平衡分布$f^{eq}$がゼロになることで、衝突項もゼロになることがわかります。
粒子速度による積分は、簡単に言うとマクロ変数への変換です。
非平衡分布$f^{neq}$という関数はマクロ的にはゼロになる成分であり、 平衡分布$f^{eq}$という関数はマクロ的には 密度という意味のある値となります。
つまり、分布関数fはマクロ的に意味のある平衡分布 $f^{eq}$ とマクロ的にはゼロとなる非平衡分布 $f^{neq}$ に分けられることになります。イメージが掴めたでしょうか?
このように直感的な理解ができるとCFDは前に進みやすいので、厳密性は若干劣るかもしれませんが直感的な想像も入れてやると勉強が楽になります。
BGKモデル(詳細)
衝突項にBGKモデルを使用した場合の格子ボルツマン方程式は下記となります。
$$ f_i(x + e_i \Delta t, t+\Delta t) – f_i (x,t) = – \frac{\Delta t}{\tau} ( f – f^{eq} ) $$
上の式は時間と空間、粒子速度で離散化されていることに注意してください。
分布関数fがxとeとtの3つの関数にも関わらずxとtの関数のように書かれているのは、右下添字が粒子速度eを表しているからです。
よってD2Q9モデルだと上記の格子ボルツマン方程式に対して i=0~8 の各方向成分を計算することになります。
右辺は衝突項$ \Omega (f)$にBGKモデルを使用しています。
$\tau$は緩和係数で、平衡状態まで変化させるのにどのくらい仮想粒子の衝突を発生させるかをコントロールする変数です。
「緩和」という名の通り、「粘度」と非常に関係があり、下記の式で表すことができます。
$$ \nu = c_s^2 (\tau – \frac{\Delta t}{2}) $$
$c_s^2$は音速パラメータであり、通常$\frac{1}{\sqrt{3}}$をとります。
上記は粘度に関する式となっていますが、当然$\tau =$の式にもできます。
つまり、粘度という物性値を与えることで、緩和係数が決まり、仮想粒子の衝突の度合いが決定されることがわかります。
平衡分布関数$f^{eq}$
衝突項$\Omega (f)$をBGKモデルで書くと下記の式になります。
$$\Omega (f) = – \frac{1}{\tau} ( f – f^{eq}) $$
分布関数fは既知の値で、$\tau$は粘度と$\Delta t$によって計算できるので、あとは平衡分布関数$f^{eq}$だけ計算できれば衝突の計算ができます。
ここでは、平衡分布関数$f^{eq}$について説明します。
平衡分布関数$f^{eq}$は下記の式で計算できます。
$$ f_i^{eq} (x,t) = w_i \rho ( 1 + \frac{u \cdot c_i}{c_s^2} + \frac{ (u \cdot c_i)^2 }{ 2 c_s^4} – \frac{u \cdot u}{ 2 c_s^2}) $$
D2Q9の場合は9方向i=0~8に対して上の式を計算することになります。
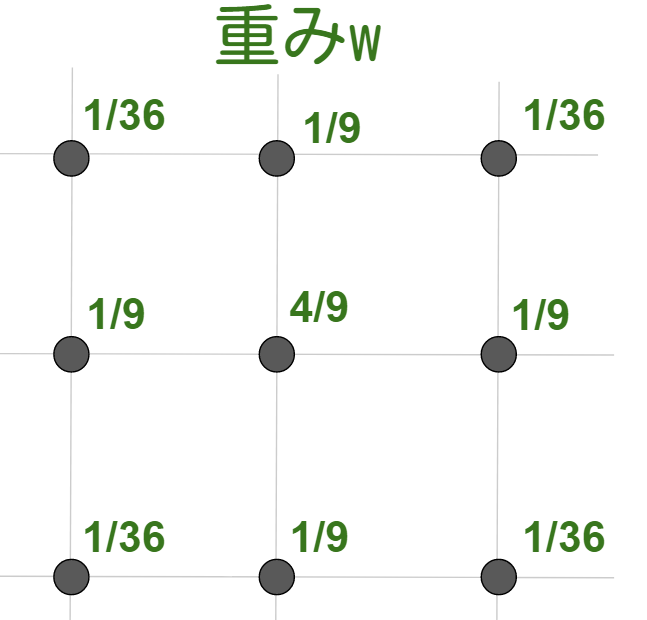
右辺の$w_i$は重み係数です。仮想粒子の方向に応じて重みが付けられます。
D2Q9モデルだと、中心が$w=\frac{4}{9}$で、縦と横が $w=\frac{1}{9}$ 、斜めが $w=\frac{1}{36}$ となっています。
$\rho$は密度、$c_s$は音速パラメータで一般的に$c_s=\frac{1}{\sqrt{3}}$が使用されます。
uは平均速度(流速)で、マクロな流れの速さです。初期値やモーメントの計算によって得られる値ですが、流入条件などを与える場合は強制的に値を代入することもあります。$u_i$はベクトルであり、2次元で2成分、3次元で3成分となります。
$c_i$は粒子速度ベクトルで、x方向成分-1~1、y方向成分-1~1の範囲で変化します。格子ボルツマン方程式は1回のステップ$\Delta t$で粒子が隣の計算点に移動するとしているため、十字方向の速度は$|c| = \pm 1$、斜め方向は $|c| = \pm \sqrt{2}$となります。
以上で平衡分布関数が得られます。
平衡分布関数が計算できれば、衝突のステップを計算することができるようになります。
$$\Omega (f) = – \frac{1}{\tau} ( f – f^{eq}) $$
おわりに
今回は衝突のステップについて重点的に解説しました。
ポイントは下記のとおりです。
- 衝突項は流体の保存に関する制約がある
- 衝突モデルで最も有名で簡単なのがBGKモデルである
- BGKモデルは単緩和時間モデル(SRT)とも呼ばれる
- 多緩和時間モデル(MRT)もあり、複雑だが数値安定性に優れる
- BGKモデルは緩和係数で流体が平衡状態になるまでの時間を設定する
- 緩和係数は粘度で決定される
- 平衡分布関数は局所的な平衡状態を表しており、マクロ的に見える流れの成分である
- 非平衡分布関数は局所的な非平衡であり、マクロ的に見えない流れの成分である
- 平衡分布関数は各方向に応じて重みがつけられる
衝突を理解する上で、平衡分布関数と非平衡分布関数の理解は欠かせません。似たような名前をしていますが、全く逆のものです。ぜひそれぞれの違いを理解しましょう。
ここまでで格子ボルツマン方程式の要素を全て理解できました。次回からは格子ボルツマン法の計算フローについて見ていきましょう。下記からどうぞ。
 ITとCFD入門サイト
ITとCFD入門サイト 

