【LBM】格子ボルツマン方程式【格子ボルツマン法講座 #3】

はじめて格子ボルツマン法を学ぶ初心者のための講座、第三回になります。

格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。

全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD（流体解析）の手法を知っておくとベターです。

前回は格子ボルツマン法のメリットとデメリットについて説明しました。下記からどうぞ。

【LBM】格子ボルツマン法のメリットとデメリット【格子ボルツマン法講座 #2】

重要なポイントは下記のとおりです。

メリット

アルゴリズムが簡単
並列性が高い
精度が高い
数値粘性がない

デメリット

メモリ使用量が多い
メッシュが均一

これらを踏まえて、格子ボルツマン法に興味を持っていただけたのであれば、そのまま読み勧めていただければと思います。

格子ボルツマン方程式

今回は格子ボルツマン方程式について説明していきます。格子ボルツマン方程式がLBM（Lattice Boltzman Method）と呼ばれるのに対して、格子ボルツマン方程式はLBE（Lattice Boltzman Equation）と呼びます。

LBEは意外とよく使われる略称表示なので、覚えておくと良いでしょう。

今回は、ナビエ・ストークス方程式と比較しながら格子ボルツマン方程式について見ていきましょう。

ナビエ・ストークス方程式

まずは、格子ボルツマン方程式との比較のためにナビエ・ストークス方程式について振り返りましょう。

ナビエ・ストークス方程式は、非定常項・移流項・粘性項・圧力項・（重力項）でできています。

$$\frac {\partial v}{\partial t}+(v \cdot \nabla )v=\frac {1}{\rho} \nabla p + { \nu \nabla^2 v}+{g}$$

各項のイメージは下記を参考にしてください。

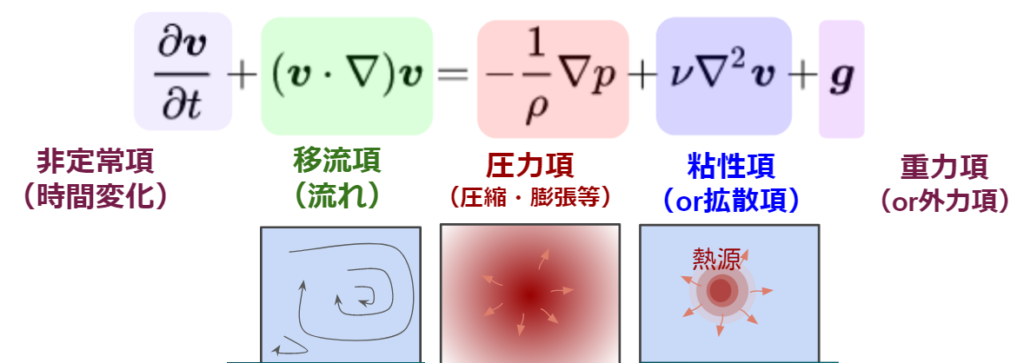
基本式は上記の通りで、場合によってはこれに外力項や表面張力項が加わることもあります。

ナビエ・ストークス方程式は一度に解くのが難しいため、「MAC法」「フラクショナルステップ法」といったように式を分割して解く方法が用いられます。

MAC法

MAC法はMarker and Cell methodの略で、一般的にナビエ・ストークス方程式の圧力項を分けて解く手法を指します。圧力を分けて解くことから「圧力分離型ソルバー」や「分離解法」とも呼ばれます。

MAC法では、ナビエ・ストークス方程式の圧力項以外を一回の計算で済ませて、圧力項の計算にはポアソン方程式で収束計算を行います。

ポアソン方程式の計算はナビエ・ストークス方程式において一番計算量が多くなりがちです。そのため、他の項と分けて計算することで行列を小さくして一度の計算量を抑えています。

フラクショナルステップ法

フラクショナルステップ法は、ナビエ・ストークス方程式を小分けにして解くという点ではMAC法と同じです。ただ、フラクショナルステップ法は圧力項以外にも粘性項や移流項を含めたほぼ全ての項を分けて計算します。

つまり、①外力、②粘性、③移流、④圧力、というように分けて計算することで個々のステップの計算量を抑えることができ、トータルでは大幅に速く計算することができます。

描画速度が求められるCG業界で使われることが多く、式を分割した分だけ精度は下がります。ただ、代わりに高次スキームを選択することで、ある程度は精度も維持することができます。

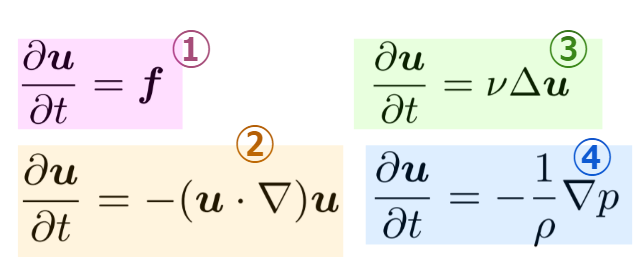
格子ボルツマン方程式

前置きが長くなりましたが、ここからは本命の格子ボルツマン方程式について説明します。

格子ボルツマン方程式は下記で表されます。

$$ f_i(x + e_i \Delta t, t+\Delta t) – f_i (x,t) = \Omega $$

左辺は衝突項で、詳細まで書くと下記のようになります。今回は深くは突っ込みません。

$$ f_i(x + e_i \Delta t, t+\Delta t) – f_i (x,t) = – \frac{\Delta t}{\tau} [ f_i (x,t) – f^{eq}] $$

構造は非常にシンプルです。左辺が並進、右辺が衝突を表しています。

fは分布関数と呼ばれ、空間xと粒子速度eと時間tの関数です。

ナビエ・ストークス方程式では流束を輸送しますが、格子ボルツマン方程式は仮想粒子としてfの並進と衝突を計算します。

また、ナビエ・ストークス方程式のフラクショナルステップ法と同様に、格子ボルツマン方程式も並進と衝突を２つのステップに分けて解きます。

具体的には、まずは並進を計算します。それによって得た値を衝突のステップで更新します。

２つのステップが終わったら、流束などのマクロな値の計算を行います。

分布関数

格子ボルツマン方程式において分布関数fは非常に重要です。

分布関数fは、分子の分布を表す関数です。分布関数fを直感的に理解するのは難しいですが、物理的には「密度を速度で割った物理量」が分布関数fであり、単位は下記で表されます。

$$ [f] = kg \cdot \frac{1}{m^3} \cdot \frac{1}{(m/s)^3} $$

$ kg \cdot \frac{1}{m^3} $が質量を堆積で割った値であり、つまり密度のことです。それを$ \frac{1}{(m/s)^3} $という仮想粒子の速度３方向成分で割ったのが分布関数fになります。

分布関数fは速度や密度の単位で構成されているので、粒子速度などの変数で積分することで、流体の密度や速度などのマクロな値を得ることができます。

マクロな値への変換

分布関数の理解を深めるためにも、先にマクロな値への変換について話しておきましょう。

CFDとして使用する以上は、格子ボルツマン方程式もマクロな物性値が入出力となります。仮想粒子を計算しているからといって、入力を仮想粒子で与えることは当然できません。

他のCFDと同様に、流束や密度が初期条件となり、各ステップにおける出力も流束と密度を計算する必要があります。

流束も密度も分布関数fの積分により得ることができます。（分布関数fを仮想粒子の速度eで積分することをモーメントを取るといいます。）

密度$\rho$は分布関数fを粒子速度eで積分することで得られます。

$$ \rho ( x,t) = \int f (x,e,t) de^3 $$

分布関数の単位が $ [f] = kg \cdot \frac{1}{m^3} \cdot \frac{1}{(m/s)^3} $　であるため、粒子速度eで積分することで$ \frac{1}{(m/s)^3} $　の部分が消えて、密度の単位 $ kg \cdot \frac{1}{m^3} $ になることがわかります。

運動量密度$\rho u$とエネルギー密度$ \rho E $も同様に下記で表されます。

$$ \rho ( x,t ) u (x,t) = \int e f (x,e,t) de^3 $$

$$ \rho ( x,t ) E (x,t) = \frac{1}{2} \int | e |^2 f (x,e,t) de^3 $$

それぞれ密度で割ることで、マクロな値である流束uとエネルギーEが得られます。

圧力は粒子速度eから平均速度（流速）uを引いた相対速度vにより、下記のように計算できます。

$$ p = \rho R T = \frac{2}{3} \rho U = \frac{1}{2} \int | v |^2 f (x,e,t) de^3 $$

Uは内部エネルギーであり、エネルギー全体から運動エネルギーを引いたものです。

vは相対速度で、下記の式で計算できます。

$$ v (x,t) = e (x,t) – u (x,t) $$

eは粒子速度で、uは平均速度（流速）です。流速を引いていることから、つまり相対速度とはマクロ的には見えない仮想粒子の速度成分とも言えます。

これにより、流速、圧力、エネルギーといったCFDで用いられている値が計算でき、格子ボルツマン方程式でも流体シミュレーションができることがわかります。

格子ボルツマン方程式

分布関数fの特性がわかったところで、再び格子ボルツマン方程式の説明に戻ります。

格子ボルツマン方程式は下記で表せることを先程説明しました。

$$ f_i(x + e_i \Delta t, t+\Delta t) – f_i (x,t) = \Omega (f) $$

しかし、これは離散化した後の式です。そのため、一度スタートに戻って連続的な式から考えましょう。

格子ボルツマン法では、分布関数fの時間変化は衝突項で表されます。

$$ \frac{d}{dt} f (x,e,t) = \Omega (f) $$

ここで、 $ \frac{d}{dt} $ は全微分なので、fの各変数に対して偏微分するように式を変形します。すると左辺は下記のようになります。

$$ \frac{d}{dt} f (x,e,t) = \frac{\partial f}{\partial t} \frac{\partial t}{\partial t} + \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial e} \frac{\partial e}{\partial t} $$

ここで、変数に置き換えられるものを書き換えると下記のようになります。

$$\frac{\partial t}{\partial t} + e \frac{\partial x}{\partial t} + \frac{F}{\rho} \frac{\partial f}{\partial e} = \Omega (f) $$

ここで、$ e = \frac{\partial f}{\partial x} $ であり、$ \frac{F}{\rho} = \frac{\partial e}{\partial t} $です。

左辺の第二項は速度eの粒子の並進（移流）を表します。そして左辺の第三項は外力による粒子速度の変化を表しており、外力がないバアはこれはゼロとなり、無視できます。

つまり、衝突項$\Omega (f)$は分布関数fの時間変化をコントロールするソース項であることがわかります。

具体的には、毎ステップで衝突が発生することで、分布関数fが再分布されるという現象が起きています。