はじめて格子ボルツマン法を学ぶ初心者のための講座、第二回になります。
格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。
全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD(流体解析)の手法を知っておくとベターです。
前回は格子ボルツマン法の基本について説明しました。下記からどうぞ。
重要なポイントは下記のとおりです。
- 統計処理した仮想粒子を計算する
- メソスケールの解析と呼ばれる
- 並進と衝突の2つのステップで計算される
- 統計処理により、規則正しい格子で計算することができる
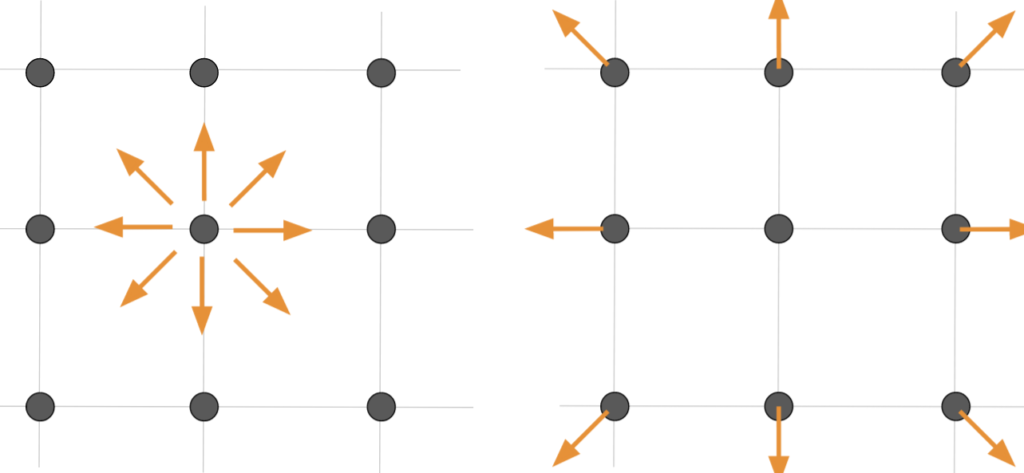
- 縦と横と斜め方向の粒子移動を計算するD2Q9モデルが使用される
格子ボルツマン法のメリット・デメリット
格子ボルツマン法(LBM)は、従来のCFDである格子法や粒子法とは異なる考え方で流体をシミュレーションする手法です。
メソスケール(マクロとミクロの間)を得意とする手法と言われており、格子を沿った粒子運動を計算するという手法であるため、かなり特殊です。
だからこそ他のCFDと比べて得意不得意がはっきりとしています。ここでは他の手法と比較するヒントとして、格子ボルツマン法のメリットとデメリットを見ていきましょう。
メリット
まずはメリットについて見ていきましょう。
簡単
アルゴリズムが簡単であることが1つ大きなメリットです。基本式は並進と衝突のステップだけなので、実装が非常に容易です。
また、格子ボルツマン法では、全ての格子点において独立して陽的に計算できるため、行列計算が不要となっています。
格子法では圧力のポアソン式で行列計算が出て来るため、この計算で苦戦します。そのため、数学的なテクニックが山のようにありますが、LBMは従来の数学的なテクニックのほとんどが不要です。
並列性
格子ボルツマン法は全ての格子点で陽的に独立して計算できるため、並列性が高いです。
一般的なCFDだとCPUで並列計算しますが、格子ボルツマン法ではGPUで計算するのが一般的です。
これは、スケーラビリティによる違いです。一般的なCFDは並列性を増やすと性能が発揮できなくなるため、一つのコア性能の高いCPUが使用されます。一方で、格子ボルツマン法はスケーラビリティが非常に高いため、GPUで計算されるのが一般的です。
CPU性能は2000年代前半から単コアの性能が伸びていないので、世の中のトレンドもあってGPU計算が強い格子ボルツマン法が着目されています。
精度が良い
格子ボルツマン法はモデル選択により精度と計算量のバランスを調整できます。
D3Q27モデルを使用すれば斜め方向の並列も捉えることになるため、格子法に比べて複雑な流れに強いといえます。
数値粘性がない
格子法のような差分法だと、移流計算に数値粘性が入ります。これは安定化のために必要で、小さくすることはできても完全に取り除くことはできません。
一方で格子ボルツマン法では、並進ステップで数値粘性が入りません。これは、並進ステップでクーラン数が必ず1になるためです。このため、流れを正確に捉えやすくなります。
デメリット
ここまではメリットについて解説してきました。多くの強みがあることから近年格子ボルツマン法が着目されていますが、当然デメリットもあります。
ここからはデメリットについて説明していきます。
メモリ使用量が多い
精度を十分に高める場合、D3Q27モデルを使用しますが、このモデルでは格子点1つにあたり 3×27=81個 のデータを必要とします。更新前と更新後のデータを保存することを考えると、データ量は 81×2 =162個 になります。
多くのメモリを使用するため、従来のCFDでは気にしていなかった部分で計算規模に制限がかかることがあります。
メッシュが均一
格子ボルツマン法では、くー乱数を1としており、時間ステップはすべての領域で均一であることから、格子間隔も均一である必要があります。
これに関しては、差分格子ボルツマン法などの研究が進められていますが、現状では基本的に均一格子が基本と思っておいて良いでしょう。
メッシュ構造の問題は境界条件にも関わっており、格子ボルツマン法は複雑な境界条件が苦手です。局面だと正しく再現できなかったり、保存されなかったりといった問題が起こります。
おわりに
今回は格子ボルツマン法のメリットとデメリットについて説明しました。
それぞれについてまとめると下記のとおりです。
メリット
- アルゴリズムが簡単
- 並列性が高い
- 精度が高い
- 数値粘性がない
デメリット
- メモリ使用量が多い
- メッシュが均一
ここでは説明していませんが、歴史が浅いというのも格子ボルツマン法のデメリットの一つです。まだ発展途上なので何が解析できて何ができないかがまだ明らかになっていません。
このあたりは時間が経てば商用ソフトウェアも増えるので、色々な業種に使用されていくでしょう。
次回は格子ボルツマン方程式とその解き方について説明します。下記からどうぞ。
 ITとCFD入門サイト
ITとCFD入門サイト 

