今回から、はじめて格子ボルツマン法(LBM)を学ぶ初心者のための講座を書いていきます。
格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。
全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD(流体解析)の手法を知っておくとベターです。
格子ボルツマン法とは?
格子ボルツマン法は「流体を仮想粒子の集合体で近似し、仮想粒子の衝突と併進を計算することで、流体をシミュレーションする手法」です。
何を言っているのかわからないと思いますが、この講座を一通り読んでいただくと、上記が格子ボルツマン法を簡潔的に説明していることがわかっていただけるようになります。
一つだけポイントを伝えておくとすれば、仮想粒子という表現がキーワードになるということです。この仮想粒子という表現は他のCFD手法にはない考え方です。仮想粒子の考え方をマスターすれば、格子ボルツマンの重要な特徴を理解したといえます。
仮想粒子について説明する前に、ナビエストークス方程式との違いを先に見ておきましょう。
ナビエストークス方程式と格子ボルツマン法の違い
CFD(流体解析)はナビエストークス方程式を使って計算されます。代表的なCFD手法として、格子法と粒子法があげられます。
粒子法は粒子を模擬して計算し、格子法は格子点を出入りする流体を計算します。しかし、どちらもナビエストークス方程式を使って計算するのは同じです。
一方で、格子ボルツマン法ではナビエストークス方程式を使いません。ナビエストークス方程式とほぼ同等の結果が得られる格子ボルツマン式(LBE)を使用します。
つまり、格子ボルツマン法の比較対象はナビエストークス方程式ということになります。
それぞれの式の特徴について見ていきましょう。
ナビエ・ストークス方程式は、「マクロな物性(粘度や圧力など)から、マクロな流れを捉える手法」です。
例えば、移流はマクロな流れそのものですし、粘度や圧力は本来は分子運動による影響ですが、マクロ的に見たときの入力と出力だけを見ています。
一方で、格子ボルツマン法は「仮想粒子というミクロな量を統計的に扱うことで、マクロな流れを捉える手法」です。
ポイントは仮想粒子というミクロな量を見ているということです。分子運動とまではいきませんが、ナビエ・ストークス方程式よりも十分小さいスケールで見ています。
細かい話をすると、ナビエ・ストークス方程式も格子ボルツマン法も移流(並進)という考え方は同じです。どちらも物性が流れに沿って移動します。
しかし大きな違いは粘性や圧力といった現象です。ナビエ・ストークス方程式は粘性や圧力といったマクロな視点で捉えるのに対し、格子ボルツマン法は仮想粒子の衝突という実現象(分子運動)に近い考え方をします。
仮想粒子とはなにか?
格子ボルツマン法の説明に仮想粒子という単語がよく出てきましたが、ここで詳細を説明します。ここまでの説明では、仮想粒子は、分子運動とまではいかなくても十分にミクロな挙動という説明でした。これはあくまでざっくりとした理解なので、きちんと理解していきましょう。
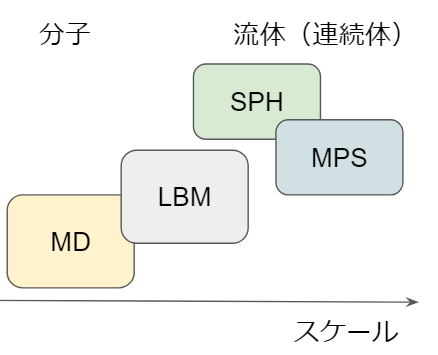
まず前提として、理想は全ての分子を捉えることです。しかし、分子を一つ一つ扱おうとすると、MD(分子動力学)のようにとんでもない計算量になってしまいます。
そこで、もう少しざっくり計算をするために、分子を統計量で表します。例えば、右方向に流れる分子はこのくらいかなー、という感じでまとめて処理することで、計算量を抑えます。
この分子を統計的に処理して得たひとまとめの固まりを「仮想粒子」と呼びます。
格子ボルツマン法がメソスケールと呼ばれる理由もここにあります。分子(ミクロ)でも流体(マクロ)でもないものを計算しているため、メソスケール(ミクロとマクロの間)を解析する手法であると言われています。
格子ボルツマン法は粒子法なのか?
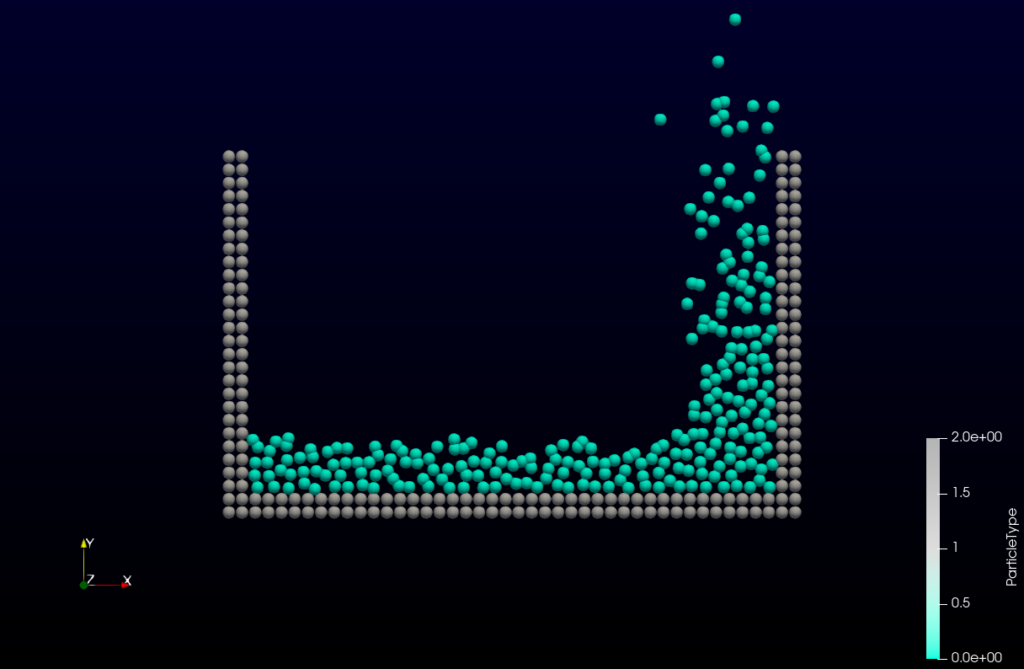
MD(分子動力学)やSPH,MPS(流体解析)をはじめとした粒子法は、粒子化した計算点を追っていく手法です。
それに対して格子ボルツマン法は、格子に固定された計算点を使って、並進・衝突を解きます。
これは粒子法というよりも格子法に近い手法です。等間隔に配置された格子において、隣接の格子点とだけ影響を与え合うというのは格子法の考え方そのものです。
粒子砲と呼ばれる理由は、仮想粒子の運動を計算するからでしょう。しかし、格子ボルツマン法は格子法として考えたほうが理解はしやすいと思います。粒子法か格子法かという議論には決着はついていないので、わかりやすいほうで捉えておくと良いでしょう。
格子ボルツマン法はなぜ「格子」なのか?
仮想粒子を扱うのに、なぜ格子ボルツマン法は「格子」なのでしょうか?
ポイントは、「統計処理」にあります。
格子ボルツマン法では、分子を統計的に処理した「仮想粒子」を扱うと説明しました。この仮想粒子は、統計処理をしているため、好きな配置にすることができます。
計算のしやすさを考えると、規則正しく直線的に動いてくれたほうがありがたいです。そのため、縦と横で規則的に(=格子状に)計算点を配置するのが最も便利であることがわかります。
B2Q9モデル
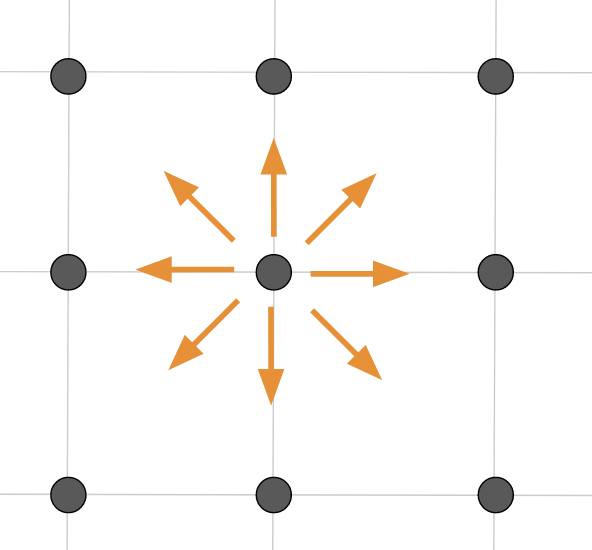
さらに、解像度は高いほうが良いので、縦と横に加えて斜めの成分も考慮することが多いです。よって二次元の場合は、周りの8方向+自分の計算点=9点を使用することで、高い精度を得ることができます。
このように2次元で9方向の並進を考えるモデルをD2Q9モデルといいます。二次元だとD2Q9モデルが使用されますが、3次元だとD3Q15やD3Q19、D3Q27などの種類があります。
これらは使用する周囲の点の数が異なります。簡単に違いを説明すると、D3Q15ははxy,yz平面などの2次元平面上での斜め方向を計算しない方法です。そして、D3Q19はxyz平面で最も遠い点(x=1,y=1,z=1で距離$\sqrt{3}$となる点)を計算しない方法です。D3Q27は周囲全ての点を計算します。
当然、計算点が多いほうが精度は上がります。
並進と衝突
ナビエ・ストークス方程式は移流と粘性と圧力という3つの要素を計算するのに対して、格子ボルツマン法では並進と衝突だけで流体をシミュレーションします。
たった2つのステップで計算できるため、非常に簡単です。ここではそれぞれのステップについて説明します。
並進
並進はナビエ・ストークス方程式の移流に当たるプロセスです。
ポイントは、仮想粒子は1回の時間ステップで周囲の点にしか移動しないことです。
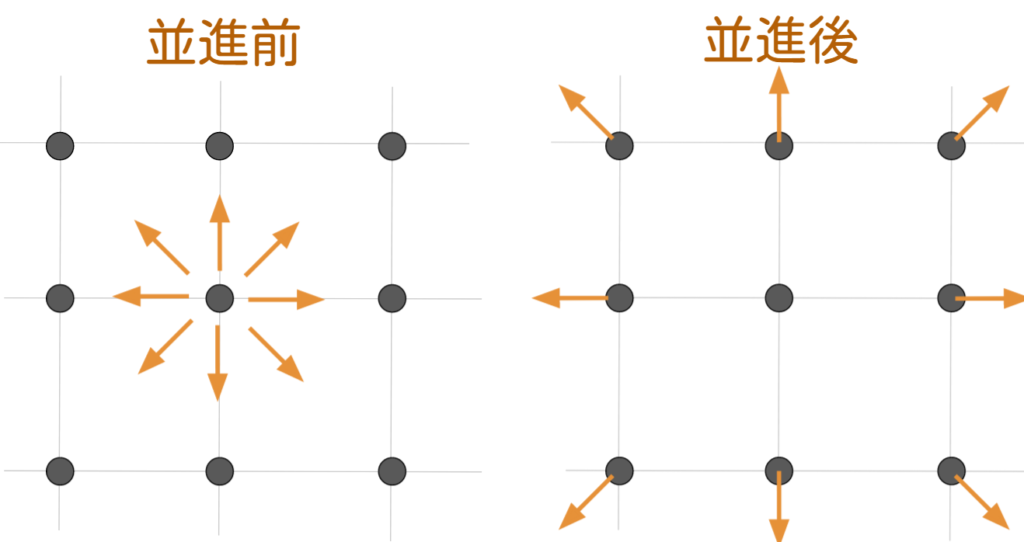
また、格子ボルツマン法では流れの方向に関係なく、全ての方向の並進を計算します。
また格子ボルツマン法では、並進のプロセスで仮想粒子がきっちり隣の格子点に移動します。つまり、クーラン数が必ず1ということになり、格子法とは少しだけ考え方は異なります。
並進は下記の図のイメージです。
衝突
衝突はナビエ・ストークス方程式の粘性と圧力に当たるプロセスです。
1回の時間ステップで1度だけ衝突計算を行います。この衝突計算では、統計処理によって得られた仮想粒子の衝突を計算しているため、分子一つ一つの衝突ではないことに注意してください。
仮想粒子に対して衝突を行うと、与えた粘性パラメータに応じて流体運動が落ち着くような挙動になります。つまり、インプットは粘性係数でアウトプットは流体の落ち着きなので、ナビエ・ストークス方程式と同じです。
格子ボルツマン法では途中計算だけが異なり、これが並列性の増加などのメリットをもたらします。
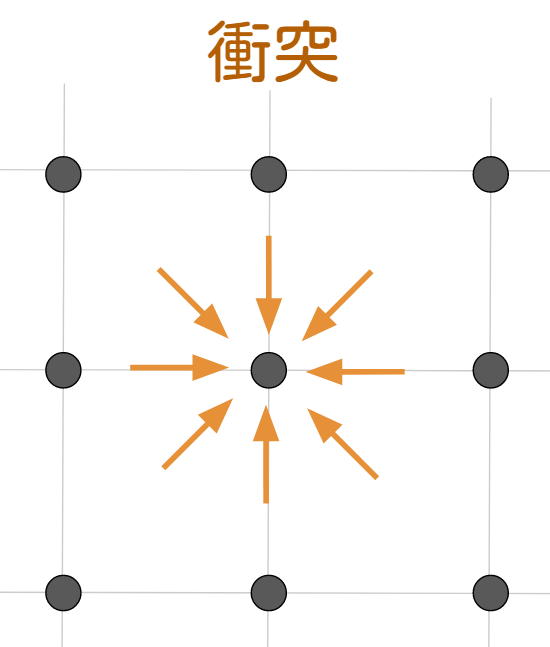
衝突のイメージは下記のようになります。
おわりに
今回は格子ボルツマン法講座の第一回として、基本について説明しました。まずは理解することを重視したため、厳密ではない部分も若干ありますが、大事なポイントは理解していただけたと思います。
格子ボルツマン法のポイントは下記のとおりです。
- 統計処理した仮想粒子を計算する
- メソスケールの解析と呼ばれる
- 並進と衝突の2つのステップで計算される
- 統計処理により、規則正しい格子で計算することができる
- 縦と横と斜め方向の粒子移動を計算するD2Q9モデルが使用される
格子ボルツマン法は、ナビエ・ストークス方程式とは異なる手法なのに同じ結果が得られるという部分で少しややこしいです。
結果はナビエ・ストークス方程式と同じになるため、格子ボルツマン法の解説において結果の話は殆どありません。
扱う対象と式が異なっているのが格子ボルツマン法のポイントです。何を扱っているかと式に関する説明がほとんどになるので、ご承知ください。
次回は格子ボルツマン法のメリットについて解説します。下記からどうぞ。
 ITとCFD入門サイト
ITとCFD入門サイト 

