クォータニオン（四元数）超入門

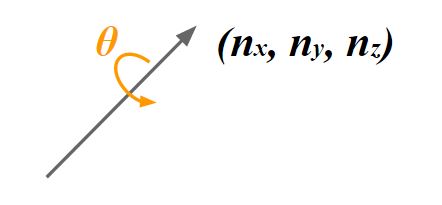
今回は３次元の姿勢制御に使用されるクォータニオンについて説明します。

２次元ではオイラー角を使用しますが、３次元ではオイラー角は複雑すぎるので多くの分野でクォータニオンの利用が推奨されます。

それは、クォータニオンを使用することで下記のメリットが得られるためです。

三角関数の利用が少ないので、計算が軽い
ジンバルロックと呼ばれる回転の特異点がない
回転行列よりも簡単

簡単に言うと、３次元の回転では２次元では想定しえなかった問題が発生するので、別の方法をとったほうが良いということです。

２次元にはオイラー角が最適、３次元ではクォータニオンが最適という風に考えると、なぜクォータニオンを学ぶのかをややこしく考えずに済みます。とりあえず３次元ではクォータニオンが必要ということですね。

オイラー角

クォータニオンの話に入る前に、オイラー角について理解しておきましょう。

オイラー角をきちんと知っておくことで、クォータニオンの理解も容易になります。

高校でもオイラー角で学ぶように、一般的に回転はオイラー角で計算するのが普通です。

例えば、２次元について$(x,y)$平面上を複素平面として考えると、角度$\theta$回転した位置$(x’,y’)$は下記式で表されます。

$$ (x’+iy’) = (\cos{\theta} + i \sin{\theta}) (x + iy) = (x \cos{\theta} – y\sin{\theta}) + i(x\sin{\theta} + y\cos{\theta}) $$

ここについてもう少し深堀りしましょう。

回転が複素平面で表せる理由は、虚数$i$が虚数部と実数部を行き来するからです。

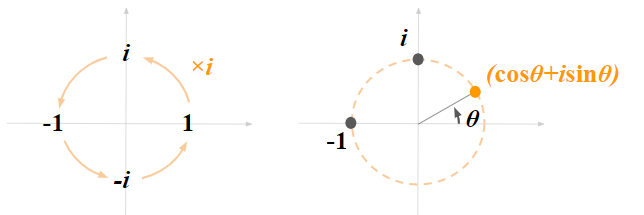
左の図で半回転$×i$は、$× \cos{\frac{\pi}{2}} + i \sin{\frac{\pi}{2}}$に相当します。これを$\theta$を使って表すと、$\cos{\theta} + i \sin{\theta}$となるわけです。

複素平面で表した回転ですが、実数部は$x$方向、虚数部は$y$方向なので行列で表すこともできます。

$$\left[ \begin{matrix} x’ \\ y’ \end{matrix} \right] =
\left[ \begin{matrix} \cos{\theta} & – \sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{matrix} \right]
\left[ \begin{matrix} x \\ y \end{matrix} \right] $$

クォータニオン

オイラー角について理解したところで、本命のクォータニオンの説明に移っていきましょう。

クォータニオンでは、上記の複素数$i$に加えて$j,k$を加えた四次元$(q = q_w + q_x i + q_y j + q_z k)$で表現します。このため、クォータニオンは四元数と呼ばれます。

（余談ですが、$w+xi+yj$の三元数では３次元の角度がうまく表現できなかったため、四元数が使われるようになったという背景があります。）

３次元を四元数で表すと当然１自由度余ってしまいますので、制限として「ノルムが１となる」という条件を与えます。これがクォータニオン（四元数）の一つの特徴です。

振り返りとして、再度クォータニオンのメリットについて振り返っておきましょう。

三角関数の利用が少ないので、計算が軽い
ジンバルロックと呼ばれる回転の特異点がない
回転行列よりも簡単

オイラー角で３次元の回転を描画しようとすると３軸全ての情報が必要になりますが、四元数であれば１つの軸$(n_x,n_y,n_z)$とその角度$\theta$だけで回転を表すことができます。

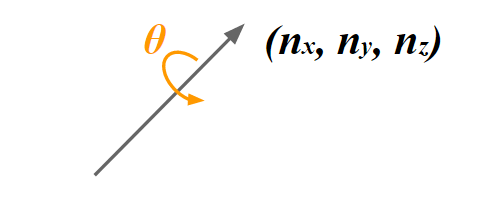
四元数として扱うことでこれらのメリットを享受できると考えると、非常に便利だということが理解できるでしょう。

クォータニオンの性質

ここからはクォータニオンの特徴について説明します。

複素平面上における虚数は$i^2 = -1$という特徴がありましたが、クォータニオンでは下記の性質を満たすように作られています。

$$i^2 = j^2 = k^2 = -1$$

$$ ij = -ji = k $$

$$ jk = -kj = i $$

$$ ki = -ik = j $$

以上の性質を満たすクォータニオンが下記で表されます。

$$q = q_w + q_x i + q_y j + q_z k$$

ここで、回転を扱うに当たり自由度を減らしたいので、ノルムが１となるような制限を加えます。

$$|| q || = \sqrt{q_w^2 + q_x^2 + q_y^2 + q_z^2}$$

クォータニオンに共役なクォータニオン$\bar{q}$も下記で定義されます。（共役なので、$q^{-1} = \bar{q}$となります）

$$ \bar{q} = q_w – q_x i – q_y j – q_z k $$

クォータニオン$q$と共役クォータニオン$\bar{q}$の２つを用いることで、任意の点に対して回転操作を行うことができます。

例えば、任意の点$r = (x,y,z)$に対して回転を与える場合は、回転後の位置$r’$は下記で表されます。

$$ r’ = qr \bar{q} $$

ここで、回転軸と角度はクォータニオン内に入っています。

もう少し詳しく見てみるために、点$r$を複素数に置き換えましょう。

$r = xi + yj + zk$に対して回転させる場合は下記式となります。

$$ x’i + y’j + z’k = (q_w + q_x i + q_y j + q_z k) (xi + yj + zk) (q_w – q_x i – q_y j – q_z k) $$

ここで、$(x’,y’,z’)$は$(x,y,z)$を軸$(q_x,q_y,q_z)$で角度$\theta$回した点です。

ここで$\theta$は$\cos{\frac{\theta}{2}}=q_w, \sin{\frac{\theta}{2}} = \sqrt{q_x^2 + q_y^2 + q_z^2}$を満たします。

つまり、クォータニオンを角度$\theta$を含む表現で書き換えると下記のようになります。

$$ q = \cos{\frac{\theta}{2}} + n_x \sin{\frac{\theta}{2}} i + n_y \sin{\frac{\theta}{2}} j + n_z \sin{\frac{\theta}{2}} k $$

ここで$n = (n_x,n_y,n_z)$は任意の軸の単位ベクトルです。

ベクトル表記に直すと下記となります。

$$ q = (\cos{\frac{\theta}{2}}, \vec{n} \sin{\frac{\theta}{2}}) $$

実部はスカラー部、虚数部$(i,j,k)$はベクトル部と呼ばれます。

上記のベクトル表示を見ると、$q_w = \cos{\frac{\theta}{2}}, \sqrt{q_x^2 + q_y^2 + q_z^2} = \sqrt{\vec{n}^2} \sin{\frac{\theta}{2}} = \sin{\frac{\theta}{2}} $ であることが明らかです。

例

以上より、クォータニオンを用いた回転について理解したので、例を用いて理解しましょう。

例えば、点$r = (r_x,r_y,r_z)$に対して軸$(1,0,0)$に$\theta_x$だけ回転して得られる$r’$は下記の式で表されます。

$$ r’ = qr \bar{q} = (\cos{\frac{\theta}{2}} + \sin{\frac{\theta}{2}} i) (r_x i + r_y j + r_z k) (\cos{\frac{\theta}{2}} – \sin{\frac{\theta}{2}} i)$$

ここでは最後まで計算しませんが、上記の点$r$に数値を入れると実際の計算が行えます。