【CFD/粒子法】粒子数密度と勾配・発散・ラプラシアン【粒子法入門 #5 MPS法編】

粒子法を用いた流体解析（CFD）の解説を行っています。第５回は、粒子数密度と勾配・発散・ラプラシアンについて解説します。

前回は粒子法の代表的な計算手法であるSPH法にとMPS法の違いと特徴ついて解説しました。まだ見てないかたは下記リンクからどうぞ。ざっくり説明すると、MPS法は非圧縮性流体を扱い、SPH法は圧縮性性流体を扱うため、色々と細かい違いが生まれますよーという話をしました。また、最近の粒子法ではどちらも非圧縮かつ安定的な解析方法が研究されていることを説明しました。

SPH法とMPS法の違いと特徴　【粒子法入門　#4】

粒子法の微分演算子

格子法では隣のセルとの差分から勾配やラプラシアンを計算することができますが、粒子法では勾配やラプラシアンなどは近傍粒子を用いて計算します。つまり、第２回で紹介した影響半径とカーネル関数は微分演算子の計算に使用されることになります。

急に知ってる前提で話されても困ると思うので、重要な部分だけ振り返っておきます。

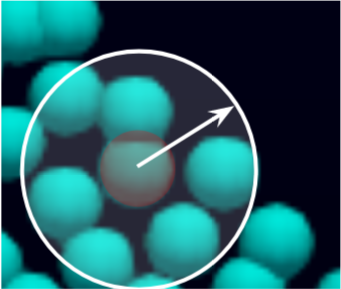
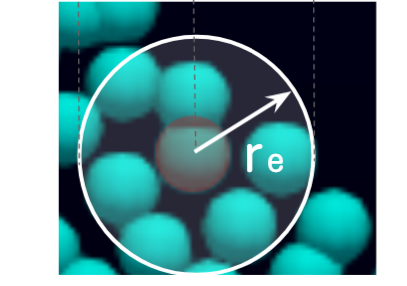
粒子法では影響半径という、粒子の相互作用を計算するための領域があります。精度と計算量のバランスから粒子径の３倍程度に設定するのが一般的です。

また、影響度は近いほうが高くなるように設定したいので、関数を設定します。これがカーネル関数です。

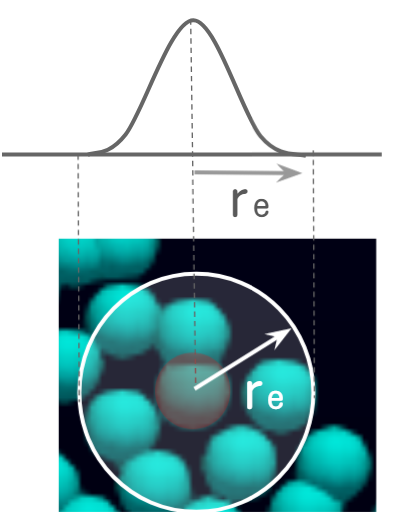
MPS法で使用されるカーネル関数w(r)は以下の式で表せます。

$ w(r) = \left\{ \begin{array}{ll} \frac{r_e}{r} & 0 \leq r \leq r_e \\ 0 & r_e < r \end{array} \right. $

rが半径でreが影響半径です。カーネル関数は中心に近いと値が大きくなり、影響半径より外だと0になります。

振り返りを済ませたところで、微分演算子について学んでいきましょう。

粒子数密度

微分演算子の計算では粒子数密度を使用するので、先に粒子数密度について説明します。粒子数密度とは、粒子の集まり具合を表す変数です。大きければ粒子がギュウギュウに詰まっており、スカスカだと密度が小さくなります。

粒子数密度は微分演算にも使われますが、他にも気液界面の判断にも使用されたりします。粒子数密度が低いということは、つまり空気と触れ合っている範囲が広いということなので、簡単に気液界面を捉えることができます。

粒子数密度は影響半径内の粒子のカーネル関数の総和で計算できます。

$$n_i = \sum_{j\neq i}w(|r_j-r_i|) $$

niは粒子数密度、$w(|r_j-r_i|)$は上記で説明したカーネル関数に対して$r$の代わりに$|r_j-r_i|$を与えることを示しています。wは変数ではなく関数なのでw×()と間違えないようにしましょう（自分はよく間違えるので…）。riは計算対象の粒子を意味しておりrjは近傍粒子です。下記のようなイメージです。

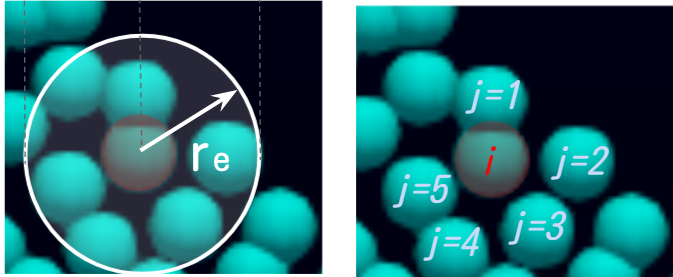
影響半径内の粒子に対してj=1,2…5の番号が振られており、これらのカーネル関数の値の総和を計算します。粒子数が多いと粒子数密度が大きくなっていくことがわかるでしょう。

ちなみにカーネル関数の引数が$r_j-r_i$の順になっているのは、$i$を基準として隣接粒子の値$j$の大きさを評価しているためです。今後もこの形で出てくるので、順番を間違えないようにしましょう。

さて、準備も済ませたところで本命の微分演算子について解説していきましょう。

MPS法の微分演算子

まずは解きたいナビエ・ストークス方程式を確認しましょう。

$$\frac {D v}{D t}=\frac {1}{\rho} \nabla p + { \nu \Delta v}+{g}$$

右辺１項目の圧力項で勾配（$\nabla$）が出てきており、右辺２項目の粘性項でラプラシアン（$\Delta = \nabla^2$）が出てきています。また、非圧縮なので、下記の質量保存に関する連続の式も満たす必要があります。

$$\nabla \cdot u = 0$$

ここで発散（$\nabla \cdot$）が出てきますので、全体として計算に必要な微分演算子は勾配（$\nabla$）、発散（$\nabla \cdot$）、ラプラシアン（$\Delta = \nabla^2$）であることがわかります。

勾配（$\nabla$）

勾配のイメージは傾きです。自分と隣の値を比較して、その傾きが勾配になります。その名の通りですね。

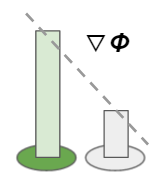
ここで使っているΦは任意の変数という意味です。実際の計算では圧力pが入ります。MPS法では勾配を下記の式で計算します。

$$ \nabla \phi = \frac{d}{n^0} \sum_{j \neq i} \frac{\phi_j – \phi_i}{ |r_j-r_i|^2 } (r_j-r_i)w(|r_j-r_i|) $$

ここで$\phi$は任意の変数であり、ナビエ・ストークス方程式では圧力pが入ります。$r_i$は計算対象の粒子位置、$r_j$は近傍粒子の位置です。下付き文字はどの粒子を指すかを表しています。w()はカーネル関数を表します。dは次元数を表しており、2次元ならd=2、３次元ならd=3となります。このように次元が増えても式が複雑化しないのも粒子法の利点です。

$n^0$は初期粒子数密度であり、式の簡単化のために粒子数密度の代わりに初期粒子数密度が使われます。初期粒子数密度は初期状態で等間隔で粒子を配置した状態で最も密な状態の粒子数密度の値になります。

ちなみに勾配を偏微分でなく$\nabla$を使う理由は、２次元や３次元を表すときにいちいちｘｙｚ方向を全部書きたくないからです。なので、単純化して考えたいときはｘ方向だけ考えると理解しやすくなります。

あと、勾配はランクが増えます。スカラー値の勾配はベクトルになり、ベクトルの勾配はテンソルになります。ナビエ・ストークス方程式を見ると圧力項がありますが、圧力がスカラー値なので圧力勾配はベクトルになっています。他にも速度がベクトルだとせん断速度（速度勾配）はテンソルになります。

発散（$\nabla \cdot$）

発散のイメージは出入りです。二次元のイメージで考えると、下記のようになります。

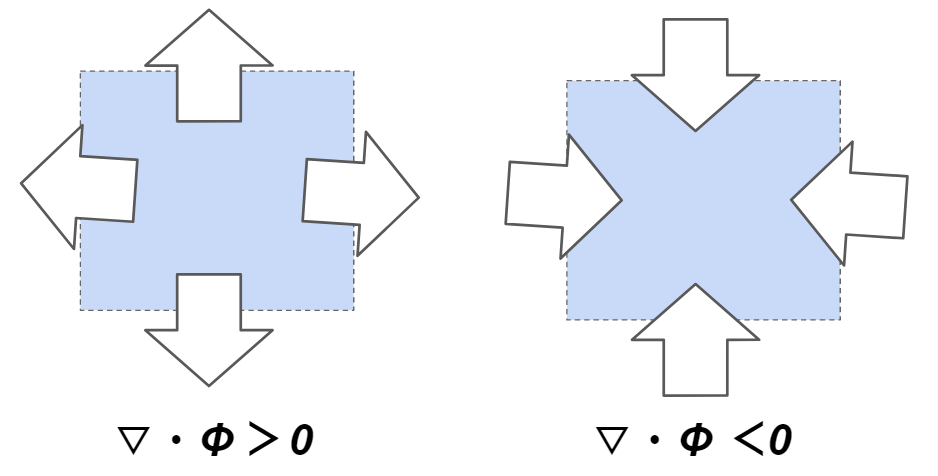
その名の通り、全ての出入り量の合計が外側に向いている（発散している）と＋になります。逆に出入り量の合計が内側に向いているとーになります。注意としては、あくまで合計量なので個々の出入り量は重要ではありません。ここで出入りとして扱っているのは、実際の値の出入りとは若干違います。これは実は勾配です。なので、発散は全方向の勾配の合計値を表します。

（非圧縮方程式で用いる連続の式では速度の発散を計算します。流体に対して上記のイメージを持つと理解しやすいです。CFDでは基本的に高い値があったら徐々になだらかになっていくので、勾配がある≒値が小さい方に移動すると考えても結構話が通ります。というか勾配を頭の中で想像するのがしんどいのでそれで良いと思います。）

数学的な記号で表すと、下記のようになります。

$$\nabla \cdot \phi = \frac{\partial \phi}{\partial x} + \frac{\partial \phi}{\partial y} + \frac{\partial \phi}{\partial z}$$

上記はｘｙｚ方向の３次元で考えた場合の発散の式です。全ての方向の微分を合計すると発散になることがわかります。

発散のイメージは割とつかみやすいと思いますが、注意点としてランクが一つ落ちることを覚えておくと良いです。今回だとベクトルｘｙｚに対して発散を計算するとスカラー値になります。せん断速度がテンソルだとせん断速度の発散はベクトルになります。

MPS法では発散は下記の式で計算します。勾配の式のΦをuに変更して∇の内積を取っただけなので詳細の説明は不要ですね。

$$ \nabla v = \frac{d}{n^0} \sum_{j \neq i} \frac{(v_j – v_i) \cdot (r_j-r_i)}{ |r_j-r_i|^2 } w(|r_j-r_i|) $$

ラプラシアン（$\Delta = \nabla^2$）

ラプラシアンのイメージは分配です。自分の値を周りに配るので、下記のようなイメージになります。

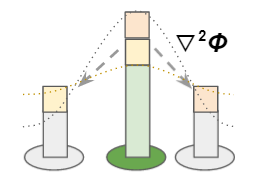
灰色のドットで描いているのが初期状態です。ラプラシアンでは値の分配を行うので、オレンジと黄色の部分を左右に分け与えています。その結果、オレンジドットの状態となり、凹凸がならされたような形状になっています。

ラプラシアンはナビエ・ストークス方程式の粘性項で使用します。粘性項では、粒子が周りに比べて遅いと、周りに引っ張られるように速度が上がります。逆に粒子の速度が速いと周りに速度を与える代わりに遅くなります。粘性項では動粘度の値でラプラシアンの効き具合を調整します。

数学的には下記のように表します。

$$\Delta \phi = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} + \frac{\partial^2 \phi}{\partial z^2}$$

イメージからはつかみにくいですが、ラプラシアンは勾配の２乗の合計です。また、ラプラシアンは勾配と発散を両方行った場合と同じ結果になります。意外ですね。そのため、ラプラシアンを行ってもランクは変わりません。勾配でランクが増えて、発散でランクが減るのでプラマイ０になるからです。

MPS法ではラプラシアンを下記の式で計算します。

$$ \nabla^2 \phi = \frac{2d}{\lambda n^0} \sum_{j \neq i} (\phi_j-\phi_i)w(|r_j-r_i|) $$

$$ \lambda = \frac{1}{n^0} \sum_{j \neq i} |r_j-r_i|^2 w(|r_j-r_i|) $$

複雑な式なのでλに分かれていますが、今までと使用している変数は一緒です。ここで$\phi$は任意の変数であり、ナビエ・ストークス方程式では圧力pが入ります。$r_i$は計算対象の粒子位置、$r_j$は近傍粒子の位置です。下付き文字はどの粒子を指すかを表しています。w()はカーネル関数を表します。dは次元数を表しており、2次元ならd=2、３次元ならd=3となります。