【LBM】固気・固液相互作用【格子ボルツマン法講座 #14】

はじめて格子ボルツマン法を学ぶ初心者のための講座、第１４回になります。

格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。

全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD（流体解析）の手法を知っておくとベターです。

前回はLBMと格子ガスオートマトン（LGA）の違い について説明しました。

【LBM】格子ガスオートマトン法（LGA）との違い【格子ボルツマン法講座 #13】

格子ガスオートマトンから格子ボルツマン法が派生したときに変更されたポイントは下記のとおりです。

平衡分布関数$f^{eq}$と重み関数を導入することで、ナビエストークス方程式を導出できるようにした
分布関数$f$の導入により、なめらかな値の変化を可能にした

これが格子ボルツマン法の特徴とも言えます。ぜひ頭の片隅に残しておくと良いでしょう。

今回は、格子ボルツマン法の固液相互作用について紹介します。

固液相互作用

今回は、格子ボルツマン法における固液相互作用（FSI:Fluid Structure Interaction）について説明します。

これまで紹介してきた境界条件は、位置が固定されているものばかりでした。そのため、キャビティ流れのように壁面に速度を与えることはできるものの、物体が流されるという挙動は解析できません。

ここでは、流体が物体に与える力と、逆に物体が流体に与える力を計算することで、固液相互作用の解析を行います。

固液相互作用により、流体内の物体移動を計算することができます。例えば、流体に沈んでいく物体や野球ボールが気流により微妙に変化する挙動などを捉えることができるようになります。

リフィル問題

計算手法について見ていく前に、固液相互作用において重要な「リフィル」について先に説明しておきましょう。

「リフィル」とは、固体通過後に現れる流体格子の扱い方に関する問題です。

CFDで動く物体を扱う場合は、流体格子に重ねることになります。例えば、格子法だとオーバーセットメッシュと呼ばれる別のメッシュを用意して、既存のメッシュに重ねる方法が取られます。

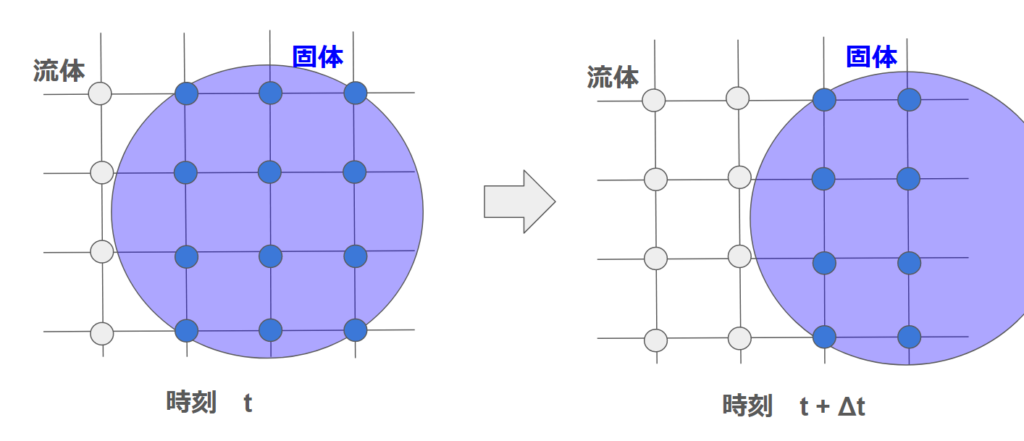
物体が動くと、上の図のように物体前方では流体格子が物体に入り込み、物体後方では流体格子が現れるという現象が発生します。

ここで、流体格子が消える分には格子点の計算を止めるだけなので問題ないですが、流体格子が現れるのは厄介です。適切な値を与えないと隣の格子との値の急な勾配により、計算が不安定になります。

そこで、この物体後方の流体格子が現れる現象＝「リフィル」をどう扱うかが固液相互作用のキモとなります。

２つの手法

格子ボルツマン法でこ液相互作用を扱う場合、大きく分けて２つの手法があります。

モメンタムエクスチェンジメソッド

一つは、「モメンタムエクスチェンジメソッド（運動量交換法）」と呼ばれる手法です。

モメンタムエクスチェンジメソッドは、今まで紹介したバウンスバックなどの壁面境界条件により、固体にかかる力を計算します。

モメンタムエクスチェンジメソッドのメリットは、壁面境界をそのまま使用できるため、高い精度をもつ壁面計算手法を利用できることです。

また、すでに学んだ知識を使えるので、学習コストも低いです。

一方でデメリットとしては、物体後方に現れる流体（リフィル）の扱いが苦手であることです。

対策として、壁から離れた格子点を３点くらい使用し、値を補間する手法が用いられます。

IBM

もう一つは、「IBM（Immersed Boundary Method）：埋め込み境界法」と呼ばれる手法です。

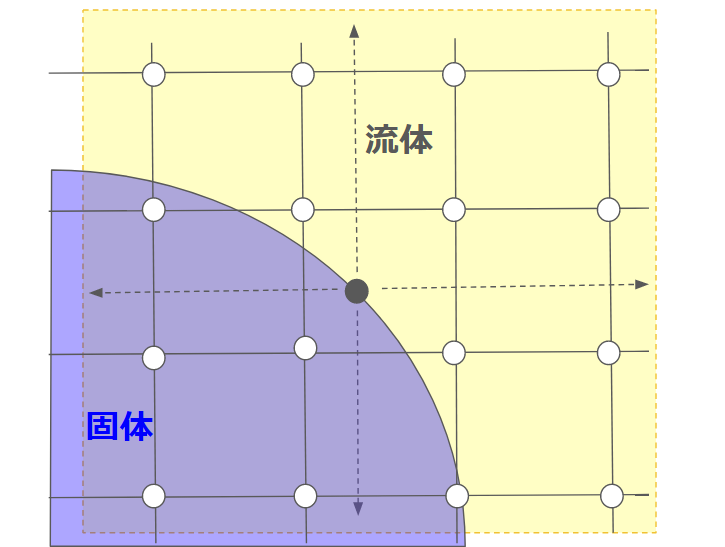
IBMは固体の中にも流体が存在するとして、領域全体の格子点で計算を行います。

IBMでは壁面境界に計算点を配置して、物体にかかる力を周りの格子点（物体内部を含む）により補間します。

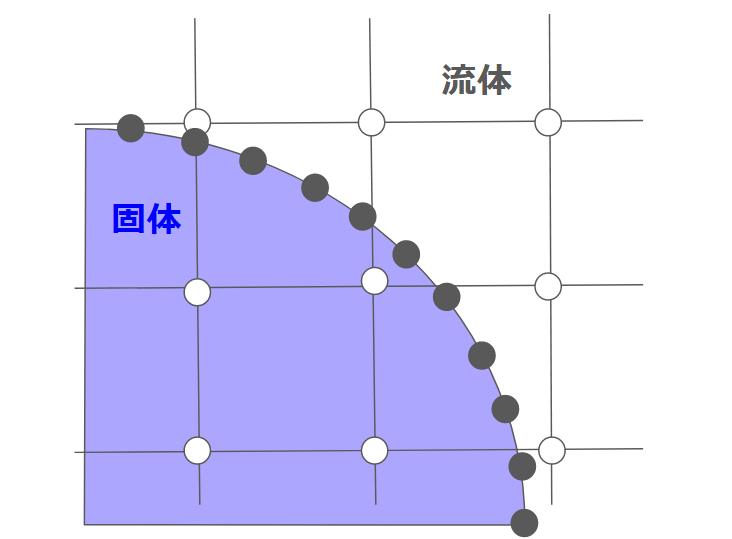
例えば上の図だと、 $2 \Delta x$ 程度の距離以内にある流体格子の値から補間して、境界の計算点にかかる力を求めます。

補間のイメージとしては、粒子法の影響半径をイメージしていただくと直感的にわかりやすいでしょう。IBMでも距離に応じて重みが付けられるようになっています。

IBMのメリットは、リフィルについて考えなくて良いことです。内部まで計算してくれているので、流体格子として現れても、それなりに妥当な値が得られます。

一方でデメリットは、補間により計算することもあり、モメンタムエクスチェンジメソッドに比べると壁面の精度が低下してしまうことです。

今回のIBMの説明では、IBMの手法の中でも一般的なダイレクトフォーシングメソッドについて説明します。

モメンタムエクスチェンジメソッドの計算手順

ここでは１つ目の手法として紹介したモメンタムエクスチェンジメソッドの詳細について説明していきます。

モメンタムエクスチェンジメソッドは、バウンスバックなどの壁面条件により移動壁面を計算し、リフィルに対しては壁から離れた点を使用して補間する手法です。

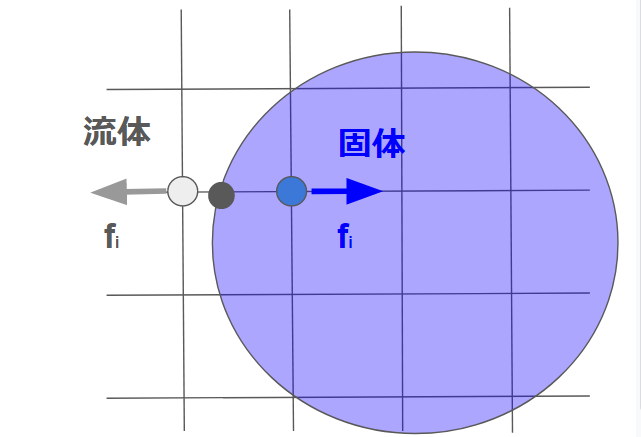
移動物体は、高い精度を維持するためにインターポレイテッドバウンスバックを使うのが一般的です。

ただし、インターポレイテッドバウンスバックを使う場合は、境界点を保持する必要があるので注意ください。

ハーフウェイバウンスバックだと境界は階段状でガタガタになりますが、$\Delta t = \Delta x$とすれば境界の保持が不要になるので実装が簡単になります。

インターポレイテッドバウンスバックを使用する場合、流体に跳ね返る分布関数$f$は下記で求められます。

$q \leq 0.5$のとき：

$$ f_{\bar{i}} (x,t + \Delta t) = (1-2q) f_i (x-1,t) + 2q f_i (x,t) – 2 w_i \rho \frac{c_i u}{c_s^2} $$

$q > 0.5$のとき：

$$ f_{\bar{i}} (x,t + \Delta t) = \frac{1}{2q} f_i (x, t) + \frac{2q – 1}{2q} f_{\bar{i}} (x – 1, t + \Delta t ) – 2 w_i \rho \frac{c_i u}{c_s^2} $$

ここで、$q$は格子点と壁の距離です。

一方でh、移動物体（固体）にかかる力は運動量の変化により求められます。

$ \delta G_p = \sum_{i} { (c_i – u_w) f_i – (c_\bar{i} – u_\bar{w}) f_\bar{i} } $

上記は、格子点１つにおける運動量の変化を計算しており、$\delta G_p$は１つの格子点にかかる力です。

よって、物体にかかる運動量はすべての壁面にかかる力の総和で求められます。格子点を$n$として下記で求めます。

$ G_p = \sum^{n} \delta G_p $

トルクは中心からの距離をかけて求めます。

$ T_p = \sum^{n} ( x – x_p ) \cdot \delta G_p $

流体のリフィルに対しても、対策が必要です。

インターポレイテッドバウンスバックを使用した場合、物体移動後に現れる流体格子に対して、物体から離れた点の値を用いて補間します。

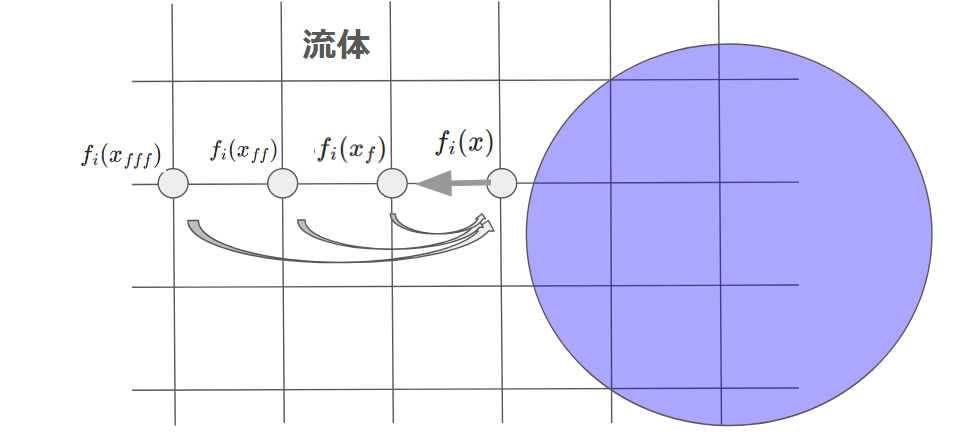
$ f_i (x) = 3 f_i (x_f) – 3 f_i (x_{ff}) + f_i (x_{fff})$

このように多くの点を使用して補間することで、振動を抑えることができます。

ただし、気液二相流なのでだとうまく機能しないので、代替する手法を用いる必要があります。

IBM（Immersed Boundary Method）：埋め込み境界法の計算手順

IBM（埋め込み境界法）は、固体内も流体で満たしてしまい、壁面境界の計算店で物体と流体の相互作用を計算します。

先に全体の流れを説明していおきましょう。

外力ありの格子ボルツマン方程式（LBM）
格子状の流速計算（LBM）
固体表面の流速の補間（IBM）
固体表面の外力補間（IBM）
格子状に外力を補間（IBM）
固体運動（IBM）

上記のように、格子ボルツマン法の計算が一通り終わったあとにIBMの計算をします。そして、次のステップで格子ボルツマン方程式に外力を上乗せするという流れになります。

１．格子ボルツマン方程式

まず、格子ボルツマン方程式を並進と衝突に分けて計算します。今まで何度も説明してきた内容なので、詳細は省略します。

$$ f_i^t (x, t) = f_i (x, t) – \frac{1}{\tau} ( f_i (x, t) – f_i^{eq} (x, t) ) + \Delta F_i (x,t) $$

ここで右辺の最後の項が外力項です。

格子ボルツマン方程式は分解して解くので、実装においては外力は並進と衝突が終わったあとに分布関数に上乗せします。

１ステップ目ではIBMの計算がまだ終えていないので、外力は初期値ゼロのままです。２ステップ目以降では前ステップでIBMにより計算された外力が与えられることになります。

ここで、外力項は $F_i =3 w_i \rho G \cdot c_i$ です。

$w_i$は重み、$\rho$は密度、$c_i$は粒子速度、$G$は後述の固体表面から補間した外力です。

２．格子状の流速計算

ここは格子ボルツマン法の基本的な部分なので、省略します。

$$ \rho = \sum f_i $$

$$ u = \frac{\sum c_i f_i }{\rho}$$

３．固体表面への流速の補間

ここからIBM特有の手順となります。

まず、流体格子から固体表面に速度を補間します。本来は格子の$\frac{1}{2} \Delta x $程度の幅で境界上に計算点を配置しますが、ここでは見やすさのために代表点１つだけで見ていきましょう。

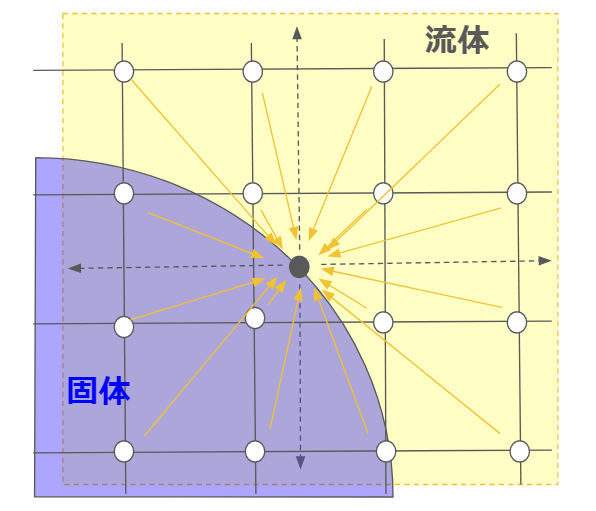
境界点の速度の補間のため、境界点から$2 \Delta x$の範囲の格子点を使用します。

境界上の計算店の速度を$u_w$とすると、下記で計算できます。

$$ u_w = \sum_{ij} u \delta (x – x_w) \delta (y – y_w) $$

補間関数$ \delta (z)$は下記で計算できます。

$$ \delta (z) = \begin{cases}
\frac{1}{4} (1 + cos(\frac{\pi | z |}{2}) & ( |z| \leq 2 \Delta x) \\
0 & ( |z| > 2 \Delta x)
\end{cases}$$

ここで、$z$は仮の変数です。実際には$x-x_w$と$y-y_w$があります。

補間関数は、粒子法でいうカーネル関数のようなものです。

距離に応じて重み付けをすることで、本来の情報を損なわずに補間を行うことができます。

４．固体表面の外力計算

外力は「ステップ３で流体から補間した固体表面上の速度」と「固体の運動により計算した速度」の差により計算します。

固体の運動はIBMの最後のステップで計算するので、１ステップ目ではまだ得られていません。よって、初期値を与えます。

初期値がゼロだと、自由に流体に流される物体の解析になります。

境界点１つにかかる外力は下記で求められます。

$$ \delta G_w = u_e – u_w $$

ここで、$u_e$は物体の運動により求めた境界点の速度で、$u_w$は流体から補間した固体表面上の速度です。

固体全体にかかる力は、境界点の値の総和で求めます。

$$ G_p = \sum^n \delta G_w \Delta s $$

$ \Delta s$は固体表面の点の間隔です。トルクも同様で、中心からの距離をかけるだけです。

$$ T_p = \sum^n (x_w – x_p) \delta G_w \Delta s $$

５．格子上に外力の補間

固体境界上の外力が得られたので、今度は格子状に補間します。

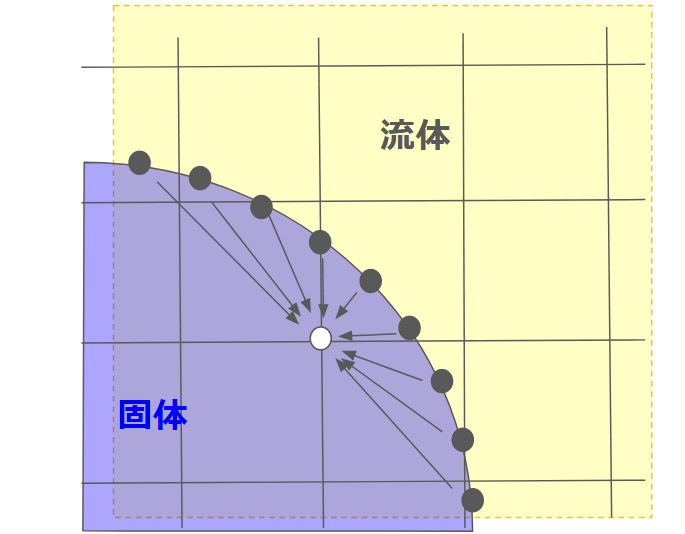
格子点から見て、$2 \Delta x$内にある協会点の値により、補間を行います。

$$ G (x) = \sum G_w \delta (x – x_w) \delta (y – y_w) \Delta s $$

$\delta ()$は補間関数、$\Delta s$は固体表面上の点の間隔です。

６．固体運動

固体運動の計算には、通常のオイラー法とは異なる特殊な手法を使用します。以下の式により、固体の運動を計算します。

$$ u_p^{n+1} = (1 + \frac{\rho_f}{\rho_p}) u_p^{n} – \frac{\rho_f}{\rho_p} + \frac{m_p – m_f}{m_p} g \Delta t + \frac{G_p}{m_s} \Delta t$$
$$ \omega_p^{n+1} = (1 + \frac{\rho_f}{\rho_p}) \omega_p^{n} – \frac{\rho_f}{\rho_p} \omega_p^{n-1} + \frac{T_p}{I_p} \Delta t$$
$$ x_p^{n+1} = x_p^n + \frac{u_p^{n+1} + u_p^{n}}{2} \Delta t $$
$$ \theta_p^{n+1} = \theta_p^n + \frac{\omega_p^{n+1} + \omega_p^{n}}{2} \Delta t $$

下添え字$p$は固体を表しており、$f$は流体です。

上添字の$n$は時間ステップで、次ステップである$n+1$を求めるために現ステップ$n$と１つ前のステップ$n-1$を使用することで、安定した値を得ることができます。

これは、アダムス・バッシュフォース法と同じ考え方です。時間方向に長めのステンシルを取っていると考えると、計算が安定するイメージがつかみやすいでしょう。

以上で、IBMを用いた固液相互作用の計算は終わりです。