【CFD/格子法】移流項の離散化【格子法入門 #6】

格子法を用いた流体解析（CFD）の解説を行っています。第６回は、移流項について解説します。

前回は陽解法と陰解法の違いについて解説しました。まだ見てないかたはこちらからどうぞ。

【CFD/格子法】陽解法と陰解法の違い　【格子法入門　#5】

ざっくり説明すると、

今回は陽解法と陰解法について解説しました。現在の時間ステップの値（n）を用いて未来の時間ステップの値（n+1）を計算する手法を陽解法といい、未来の時間ステップの値（n+1）を用いて未来の時間ステップの値（n+1）を計算する手法を陰解法といいます。陰解法では収束計算を使用するので、クーラン数に関するCFL条件や拡散数の条件が当てはまらなくなります。時間ステップを多少大きめにとっても計算ができるので、広く使用されていることを解説しました。

移流項とは？

まずは移流項とは何かについて振り返りましょう。CFDでは、ナビエ・ストークス方程式を使用して流体の流れを計算します。

$$\frac {\partial v}{\partial t}+(v \cdot \nabla )v=\frac {1}{\rho} \nabla p + { \nu \nabla^2 v}+{g}$$

左辺の第一項が非定常項と呼ばれ、時間変化を表します。第二項は今回の主題の移流項で、流体の流れによる移動を扱います。右辺の第一項第一項が圧力項と呼ばれる圧力が流れに影響を与える項です。右辺の第二項が粘性項と呼ばれる粘性が流れに影響を与える項です。そして、最後が重力項です。

各項のイメージは下記のとおりです。

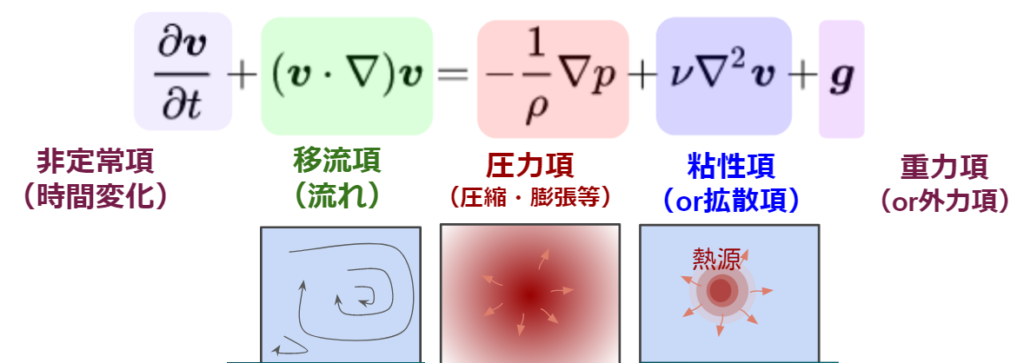
第三回で非定常項と粘性項を例に離散化の紹介を行いました。また、第４回で圧力分離型ソルバーを例に圧力のポアソン方程式を紹介しました。つまり、ここまでの解説で非定常項・圧力項・粘性項の説明は終えているということです。詳しく知りたい方は過去の記事をご確認ください。

残るは移流項と重力項ですが、重力項は特に説明するほど難しいものではないので、今回の移流項をマスターすればナビエ・ストークス方程式の離散化についてマスターしたと言ってもいいでしょう。

移流項の離散化（中心差分）

今回は移流項を扱うので、ナビエ・ストークス方程式の左辺第二項に着目します。三次元だと下記のように表せます。

$$ (v \cdot \nabla )v = u\frac{\partial u}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial w}{\partial z} $$

左辺の発散（∇・）は各方向に対する微分の合計になります。ご覧の通り、三次元だとどうしても項が多くなりますので、今回はｘ方向だけを考えた一次元で解説を進めます。具体的には、一次元の移流項として下記を使用します。

$$ (v \cdot \nabla )v = u\frac{\partial u}{\partial x} $$

それでは早速離散化について学びましょう。離散化とは、連続的なデータを離散的なデータに変換することでした。ナビエ・ストークス方程式では移流項はｘｙｚ空間に対して微分されているので、格子法では格子を用いてこの微分を離散化します。

周りの点から計算点を計算するために、一番はじめに思いつくのが周囲の点の値の平均を取ることでしょう。今回は微分、つまり勾配を表す必要があるので、周囲の点で勾配を表します。図で表すと下記のようなイメージです。

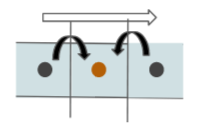
式で表すと下記のようになります。

$$u\frac{\partial u}{\partial x} = u_i \frac{u_{i+1}-u_{i-1}}{2\Delta x}$$

ここで、$u_i$は計算点、$u_{i+1}$は右隣りの点、$u_{i-1}$は←隣りの点、$\Delta x$はセルの大きさを表します。微分で表していた部分が離散化によって一つ飛んだセルの差分になっていることがわかります。

この方法は、周りの点の値を参照してちょうど中心にある点を計算するので、中心差分と呼ばれます。

中心差分の一番のメリットは単純な式なのに誤差が小さいことです。直感的に理解できるし、おそらく何も無い状態だったら誰でもこの式を思いつくのではないでしょうか？

ただし、格子法で移流項が難関と言われている理由は中心差分のデメリットにあります。中心差分のデメリットとして何より問題なのは、値が振動して現実的に使用できないということです。

せっかく学んだ中心差分ですが、解析では全く役に立ちません。そのため、日々研究者たちが誤差と安定性をバランスさせる様々な離散化手法を検討しています。今回は、具体的にどのような手法があるのか一例をお見せしたいと思います。

移流項の離散化（風上差分）

風上差分は最も安定であると言われている移流項の離散化手法です。

風上差分は流れの風上型の値を参照して差分を行います。参照店の位置が流れの向きに影響を受けるのが特徴です。下記のイメージです。流れによって条件を変える必要があることがわかります。

風上差分は安定性は高いですが誤差も大きく、先ほど紹介した中心差分が二次精度（⊿xの２乗に比例した誤差が発生する）だったのに対して、風上差分は一次精度（⊿xに比例した誤差が発生する）です。

一次と二次だとあまり違いがないように感じるかもしれませんが、一桁の差は大きいです。粘性項が二次精度の離散化なので、移流項が一次精度か二次精度どちらを選ぶかによって計算結果の質が大きく変わります。一般的には二次精度が推奨されているので、風上差分はあくまで練習やテスト用で、実用的な使われ方はされていないのが現状です。

風上差分の式は下記の通りです。

$ u\frac{\partial u}{\partial x} =
\begin{cases}
u_i \frac{u_{i+1}-u_{i}}{Delta x} & u_i \leq 0 \\
u_i \frac{u_{i}-u_{i-1}}{Delta x} & u_i > 0
\end{cases} $

風上がどちらであるかを流速の符号で判断します。一つの式にまとめることもできるのですが、ここではわかりやすく条件分けしています。

特徴としては、風上差分では隣り合ったセルを参照する形になっていることです。中心差分では不安定だったのが風上差分では安定するのは、隣り合ったセルを参照することが一番の理由です。中心差分では一つ飛ばしでセルを参照することになるので、Vの字の形で値が変動した場合は勾配を捉えきれません。その結果、変動が増大して発散します。一方で、風上差分は小さな変動でも捉えきれるので、安定して解析できます。

ただし、先述したように風上差分は誤差が大きいので実用的ではないです。一方で、安定性は最も高いのでCFDコードのテストにはよく使われます。今後最も触れることの多い離散化手法になると思います。

移流項の離散化（高次多項式）

今までは離散化に１次の差分を使用していましたが、高次多項式を使えばさらなる高精度化を狙うことができます。

高次多項式とは、ｘの二乗や三乗等を含んだ式のことです。微分は簡単には離散化できませんが、高次の項が増えることで情報が増えて、基の連続的な微分を再現しやすくなります。テイラー展開がわかりやすい例ですね。

ここでは、Lax-Wendroff法について紹介します。

Lax-Wendroff法は、二次多項式を使用することで振動を抑制する手法です。中心差分をもとにして、２次の拡散項が入ることで安定性が増しています。

風上差分で安定化する理由として、セルをまたいでいないことを説明しました。しかし、風上差分が安定する理由として、もう一つあります。それは、中心差分に拡散を加えた形になっているからです。風上差分の式を整理するとわかりますが、長くなるのでここでは省略します。拡散を加えることで、中央差分によって生まれる振動を押さえつけているのです。

Lax-Wendroff法も同じ仕組みです。風上差分では拡散が大きすぎて現実離れした結果となってしまうので、二次の項を使うことで適度に安定化を和らげたと思って頂ければ良いかと思います。

Lax-Wendroff法の離散化は下記のようになります。

$$u\frac{\partial u}{\partial x} = u_i \frac{u_{i+1}-u_{i-1}}{2\Delta x} + {u_i}^2 \Delta t \frac{u_{i+1}-2u_{i}+u_{i-1}}{2{\Delta x}^2}$$

右辺第一項が中心差分で使用したものと全く同じであることが分かると思います。そして、右辺第二項が二次の拡散項です。ここで拡散を与えることで、中心差分で発生していた計算不安定を和らげることができています。

他にも高次多項式による離散化手法は多くあります。需要と機会があれば記事化します。QUICKやWENOなんかがよく使われる印象があります。

高次風上
QUICK
QUICKEST
河村・桑原スキーム
ENO
WENO

移流項の離散化（その他）

移流項の離散化は長年悩まれてきた問題です。多項式を使えばすぐに解決とはなりません。

そのため、他にも様々な離散化方法が研究されています。ここでは離散化手法の中でも有名なものを２つ簡単に紹介します。

CIP法

CIP法（Constrained Interpolation Profile scheme）は計算点の値とその傾きを使用することで高精度にした手法です。

中心差分で計算不安定になる原因は、飛び飛びの値を使用しているためでした。値がV字型になると不安定になんだったら、傾き情報も使って安定化させてやろうというのがCIP法です。イメージとしては下記のようになります。

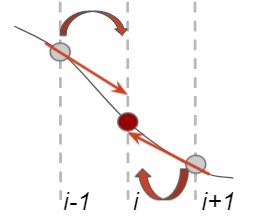
両隣の値の情報＋両隣の値の傾き情報、つまり計４つの情報を使用することで高精度かつ安定を実現しています。実際使ってみると、かなり優秀です。

ただしデメリットもあり、二次元以上では式がとても複雑になることです。また傾きを使用するため、必要な情報が単純に二倍になります。背に腹は変えられませんが、これらのデメリットを考えて導入を検討すると良いでしょう。

ちなみにCIP法の発展として、RCIP法と呼ばれる計算不安定によるオーバーシュートを抑えた手法や、CIP－CSL法と呼ばれる体積保存を考慮した手法などがあります。

セミラグランジュ法

セミラグランジュ法はその名の通り、ラグランジュ的に移流項を求める方法です。

先にオイラー法とラグランジュ法を説明しておきましょう。オイラー法は計算点が固定されていて、流体が流れます。一方でラグランジュ法では計算点が流体と一緒に流れます。つまり、格子法はオイラー法で粒子法はラグランジュ法というわけです。

今までは隣の格子から流れてくる流体を計算するというオイラー的な解き方をしていました。一方で、セミラグランジュ法はラグランジュ的に計算するので、大きく異なります。

手順としては下記の３ステップで移流を計算します。

計算点xから-u方向にΔtだけバックトレース
速度場u(x_bt, t)を周りの値から補間
速度場u(x_bt, t)を次のステップの速度場u(x, t+Δt)とする

特に意識してほしいのは、手順の１番です。流れ場を使ってラグランジュ的に上流を推定することで、次のステップにおける流速を計算しています。セミラグランジュ法は今まで紹介した手法とは全く違う手法と言えます。

余談ですが、セミラグランジュ法は計算が速いので、CG系でも使われたりします。現在の流体CGでは粒子法が一般的ですが、格子法で計算している人も少なからずいます。セミラグランジュ法の高速計算という特徴にはそれなりにニーズがあることがわかりますね。

おわりに

今回は格子法における一番の山鳩も言える移流項について解説しました。移流項において重要なのは、精度の安定性のバランスですが、これが非常に難しいです。

中心差分では精度は良いけど安定性がダメで、風上差分では安定性は良いけど精度がダメです。そのため、Lax-Wendroff法のような多項式による計算やCIP法・セミラグランジュ法などの特殊な手法が研究されています。

今回は説明に入れませんでしたが、TVD法という今まで紹介した手法を上手くブレンドして安定性と精度を上げる手法なんかもあったりします。（厳密には輸送性に基づく式で安定性と精度を維持しているのですが、ざっくり理解するなら中心差分や風上差分、QUICK法などをいい感じにブレンドする手法と考えてもらっても良いでしょう。）

今回でひとまず格子法入門は終わりです。格子法の特徴とナビエ・ストークス方程式の離散化手法、そしてナビエ・ストークス方程式を解く際の手順について説明しました。一通り見れば格子法の基本は身についたはずです。

CFDプログラミングにも興味がある人のために、いずれプログラムも公開します。そちらもご期待ください。

次回は乱流モデルの解説です。下記からどうぞ。