【CFD/格子法】圧力分離型ソルバー（MAC法）【格子法入門 #4】

格子法を用いた流体解析（CFD）の解説を行っています。第４回は、圧力分離型ソルバー（MAC法）について解説します。

前回は離散化と差分法について解説しました。まだ見てないかたはこちらからどうぞ。ざっくり説明すると、離散化を行うことで現実を模擬した式をPC上で計算することができるようになります。時間を離散化して時間変化を計算する非定常計算を行うことができ、空間を格子で離散化することで現実的な計算量で流体の動きを解析することができるようになる、という話をしました。

差分法と離散化　【格子法入門　#3】

非圧縮ナビエ・ストークス方程式

CFDでは下記のナビエ・ストークス方程式を解くことで流体の移動を計算します。

$$\frac {\partial v}{\partial t}+(v \cdot \nabla )v=\frac {1}{\rho} \nabla p + { \nu \nabla^2 v}+{g}$$

各項のイメージは下記を参考にしてください。

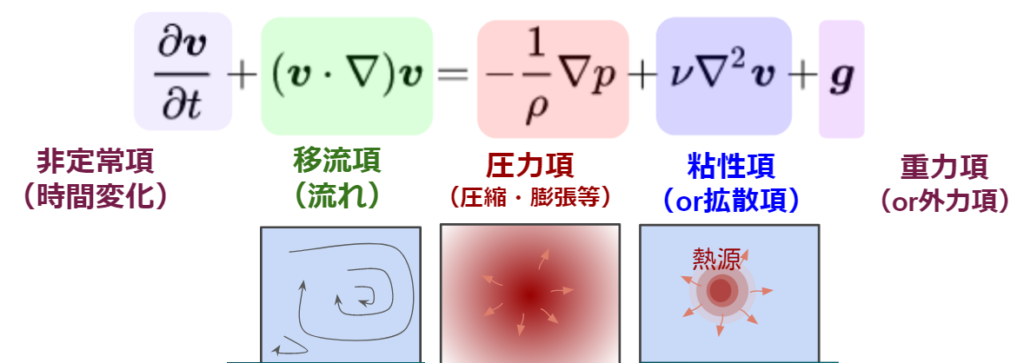
しかし、ナビエ・ストークス方程式には一般解がないので、この式は解けません。非圧縮計算では下記の連続の式と組み合わせて解きます。

$$\nabla \cdot v = 0$$

下記が圧縮に関するイメージ図です。

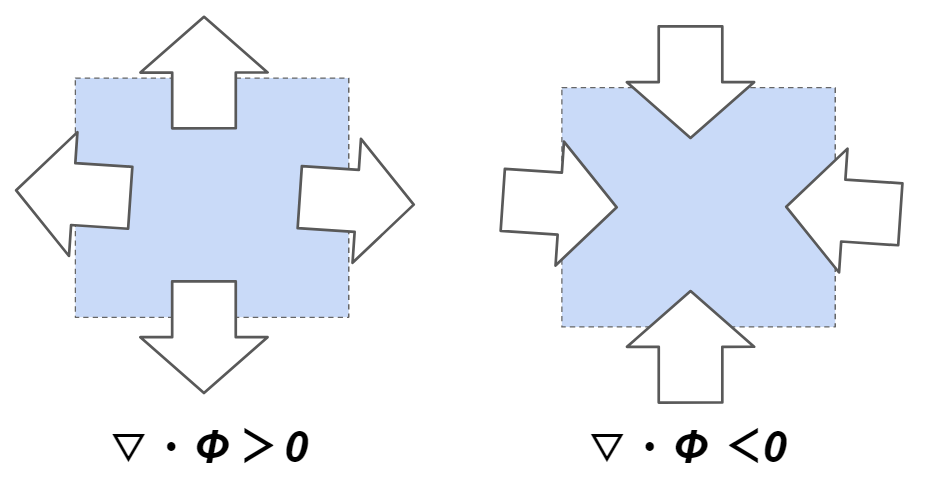
ここでは圧縮と膨張の例を書いていますが、連続の式は非圧縮に関する式なので、単位体積あたりの流入量と流出量が同じになります。つまり、外向き矢印と内向き矢印が釣り合うということです。

この２つの式を組み合わせて解く方法として、圧力分離型ソルバーが一般的です。

圧力分離型ソルバー

圧力分離型ソルバーはMAC法とも呼ばれます。圧力を先に計算して後で速度を計算する場合もありますし、その逆の場合もあります。今回は先に圧力を計算する方法で解説します。

MAC法（Marker And Cell method）は従来はマーカーを使って気液界面を計算しようという手法でしたが、圧力を分離して解くという方法が革命的過ぎたので、今となっては圧力分離型ソルバーの一般名として使われています。SMAC法（Simplified Marker And Cell method）という手法もあり、今ではこちらのほうが一般的だと思います。分離解法とか呼ばれることもありますが、やってることは全部圧力を分離して計算しており、中身は同じです。

フラクショナルステップ法とかもありますが、圧力分離型ソルバーの延長と考えてください。圧力項は分けないと普通は計算できません。フラクショナルステップ法は、その感覚で粘性項などの他の項も分けて解いちゃえ！という方法です。全ての項を分けて解くと、行列計算の収束性が上がるので計算が速くなります。

今回解説するのは、圧力分離型ソルバーとして一番基本のMAC法についてです。

MAC法（Marker And Cell method）

ナビエ・ストークス方程式の両辺に発散をかけて、連続の式に基づく置き換えを行うと、下記のポアソン方程式が得られます。

$$\nabla^2 p = \frac{\rho}{\Delta t}\nabla \cdot v$$

参考として二次元で離散化した式も下記に載せておきます。かなり難しいですが、離散化のイメージを掴むのに役立つと思います。

$$\begin{split}
p_{i,j}^{n} = & \frac{\left(p_{i+1,j}^{n}+p_{i-1,j}^{n}\right) \Delta y^2 + \left(p_{i,j+1}^{n}+p_{i,j-1}^{n}\right) \Delta x^2}{2\left(\Delta x^2+\Delta y^2\right)} \\\
&-\frac{\rho\Delta x^2\Delta y^2}{2\left(\Delta x^2+\Delta y^2\right)} \\\
& \times \left[\frac{1}{\Delta t}\left(\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right)
-\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x}\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x} -2\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x}-\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right]
\end{split}$$

ポアソン方程式では、隣接したセルの圧力から参照セルの圧力を求めます。さらに流体の速度も圧力の発生要因になります。隣接セルの圧力と速度が圧力に影響していることを意識して上記の離散化式を見て頂くと、圧力に関する項と速度に関する項の塊があることが分かると思います。

上記の圧力計算は収束計算を行います。なぜかというと、参照しているセル（i）の圧力値を変更すると、隣のセル（i+1）の圧力計算時に今のセル（i）が参照されるため、繰り返すたびに計算結果が変わるからです。よって、圧力値の変化が落ち着くまで収束計算をしないと正しい値は得られません。

圧力が求まれば、次はナビエ・ストークス方程式に代入して計算をします。

$$\frac {\partial v}{\partial t}+(v^n \cdot \nabla )v^n=\frac {1}{\rho} \nabla p^* + { \nu \nabla^2 v^n}$$

上記のナビエ・ストークス方程式を離散化します。重力項は式が長くなるので省きます。

$$\begin{split}
& \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = \\\
& \qquad -\frac{1}{\rho}\frac{p_{i+1,j}^{*}-p_{i-1,j}^{*}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}\right)
\end{split}$$

$$\begin{split}
&\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = \\\
& \qquad -\frac{1}{\rho}\frac{p_{i,j+1}^{*}-p_{i,j-1}^{*}}{2\Delta y}
+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)
\end{split}$$

ポアソン方程式で更新した値を仮の圧力値（＊）として表しています。その他の変数は現在のステップ（ｎ）の値を使用します。

非定常項と粘性項は第３回で解説した離散化が適用されていることが分かると思います。ここで引っかかると後で辛いので、わからない場合は一旦戻って確認してみてください。圧力項と移流項の離散化についてはまだ解説してませんが、今回は圧力項は中心差分、移流項は風上差分を使用しています。

軽く中心差分と風上差分についてもざっくり説明しておきます。中心差分は両隣の隣接セルを参照して計算を行う方法であり、精度は高いが不安定です。一方で、風上差分は自分のセルと流れの風上側にあるセルを参照する方法であり、安定性は高いですが誤差が大きいです。