【CFD/格子法】差分法と離散化【格子法入門 #3】

格子法を用いた流体解析（CFD）の解説を行っています。第３回は、差分法と離散化のメリットについて解説します。

前回は格子法のメリットについて解説しました。まだ見てないかたはこちらからどうぞ。ざっくり説明すると格子法のメリットとして、格子の大きさを局所的に変えられることと気液相互作用が計算できることを上げました。

【CFD/格子法】格子法のメリット　【格子法入門　#2】

離散化

まずは離散化について学びましょう。

CFDでは、ナビエ・ストークス方程式を使用して流体の流れを計算します。

$$\frac {\partial v}{\partial t}+(v \cdot \nabla )v=\frac {1}{\rho} \nabla p + { \nu \nabla^2 v}+{g}$$

各項のイメージは下記を参考にしてください。

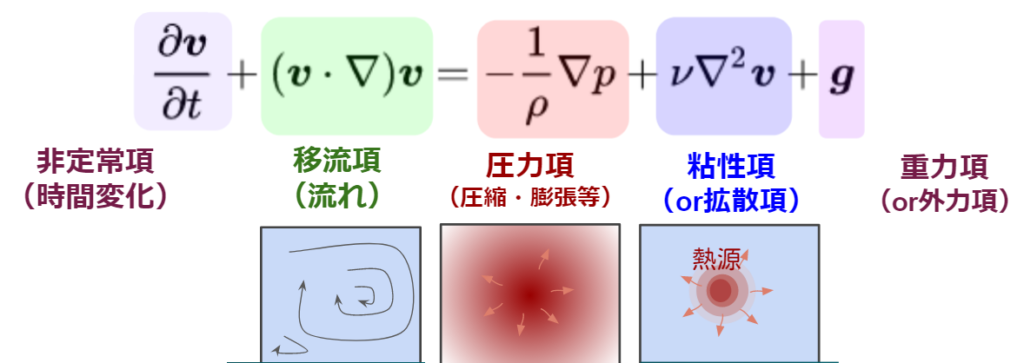
しかし、このナビエ・ストークス方程式は連続体を扱うのでPC上で計算できません。連続体とは、液体や気体のような区切りがはっきりとしないものです。それに対してPC上で処理できるのは０と１の計算だけなので、連続体は扱えません。

そこでこのナビエ・ストークス方程式を離散化する必要があります。差分法もざっくり説明すると、格子で離散化した流体流れを解くという手法なので、離散化を理解すれば差分法はほぼ理解できたと言っても過言ではないです。

時間の離散化

まずは時間の離散化について考えましょう。ナビエ・ストークス方程式には非定常項という時間微分の項があります。これを時間ステップで離散化すると下記のようになります。

$$\frac{\partial v}{\partial t}\approx \frac{v(t+\Delta t)-v(t)}{\Delta t} $$

$\Delta t$は時間ステップと呼ばれ、未来と現在の時間の差分を表します。CFDでは微小な時間ステップで解析を行い、それを何度も繰り返すことで時間変化の解析を行います。分子の$v(t+\Delta t)-v(t)$は速度の時間変化です。ここでは離散化による速度差分となっているので、微小な時間ステップでの速度変化を計算することになります。

この時間を極限まで小さくすることで、実質的に連続的な式と同じ結果が得られます。そのため、離散化した式でも十分に小さいステップを使用することで、限りなく正しいナビエ・ストークス方程式の解が得られることになります。

時間は一般的に上付き添字で表示します。

$$\frac{\partial v}{\partial t}\approx \frac{v^{n+1}-v^n}{\Delta t} $$

現在のステップをnステップ、次のステップをn+1で表します。

空間の離散化

次は空間の離散化について考えましょう。格子法では既に格子で空間を離散化しているのでイメージしやすいと思います。セルは隣り合っているので、i=1,2,..というように数えることができます。ここでは粘性項を例に考えましょう。

粘性項は１次元で考えると下記のように表せます。つまり、今回は速度の二階微分の計算の仕方が分かればゴールとなります。

$${ \nu \nabla^2 v} = \nu \frac{\partial^2 v}{\partial x^2}$$

粘性項の離散化に取り掛かるにあたって、まずはテイラー展開をします。下記のテイラー展開の式にある下添え字のiは現在参照しているセルの値、i+1とi-1は両隣のセルの値を参照することを意味します。

$$v_{i+1} = v_i + \Delta x \frac{\partial v}{\partial x}\bigg|_i + \frac{\Delta x^2}{2} \frac{\partial ^2 v}{\partial x^2}\bigg|_i + \frac{\Delta x^3}{3!} \frac{\partial ^3 v}{\partial x^3}\bigg|_i + O(\Delta x^4)$$

$$v_{i-1} = v_i – \Delta x \frac{\partial v}{\partial x}\bigg|_i + \frac{\Delta x^2}{2} \frac{\partial ^2 v}{\partial x^2}\bigg|_i – \frac{\Delta x^3}{3!} \frac{\partial ^3 v}{\partial x^3}\bigg|_i + O(\Delta x^4)$$

$v_{i+1}$と$v_{i-1}$は上記のテイラー展開で計算できます。テイラー展開がよくわからない方のためにイメージだけ伝えておくと、どんな関数でも高次の微分を足していけば表現できることを示しています。今回は$\Delta x^4$以上の高次項を$O(\Delta x^4)$と表記して無視しているので、細かい変化は計算できないことがわかります。

上記の$v_{i+1}$と$v_{i-1}$を足すと下記のようになります。

$$v_{i+1} + v_{i-1} = 2v_i+\Delta x^2 \frac{\partial ^2 v}{\partial x^2}\bigg|_i + O(\Delta x^4)$$

奇数の次数が消えてすっきりしました。ここまで来たら後は速度の二階微分を求める式に直すだけです。

$$\frac{\partial ^2 v}{\partial x^2}=\frac{v_{i+1}-2v_{i}+v_{i-1}}{\Delta x^2} + O(\Delta x^2)$$

最後の$O(\Delta x^2)$は$\Delta x^2$に比例した項を意味します。一般的には精度より計算速度を重視して$\Delta x^2$の項を無視します。理由としては、粘性項よりも誤差を引き起こす項があり、そこに計算リソースを割きたいからです。$\Delta x^2$を無視するので、この式は二次精度と呼ばれます。

おわりに

今回は格子法の核となる離散化と差分法について紹介しました。離散化には時間の離散化と空間の離散化があり、非定常項と粘性項を例に離散化を行いました。

特に意識してほしいのは、概念と数式をつなげることです。非定常計算と呼ばれる時間変化を計算するために、非定常項の離散化が必要です。流体という連続体を計算するためには、格子で分割して空間を離散化することが必要です。このようになぜ離散化する必要があるのかを理解していただくと、格子法以外にも応用の効く一生モノの知識となるでしょう。

次回はMAC法とも呼ばれる圧力分離型ソルバーについて紹介します。