【CFD/格子法】格子法と粒子法の違い【格子法入門 #1】

今回から格子法を用いた流体解析（CFD）の解説を行っていきます。第一回は、粒子法と格子法の違いとその特徴について解説します。

格子法とは？

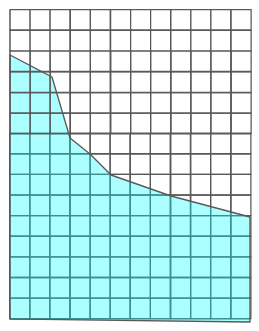
格子法とは、領域を格子で分割して流体の動きを解析する手法です。下記の図のように細かくメッシュを区切ることで、流体の小さな動きも捉えることができるようになります。

格子法は、単相流と混相流という２つの分野に大きく分けることができます。

単相流というのは、領域全てが１つの相で満たされている状態を指します。相とは気相・液相・固相のどれかのことです。流体解析では気相と液相を扱います。単相流では、気相ですべてが満たされている状態もしくは液相で全てが満たされている状態を扱います。実用性が低そうに思えますが、意外と活用範囲は広いです。

具体的には、飛行機の羽やドローンのプロペラ周りの空気の流れを解析することで、省エネで効率的な羽の設計を行うことができます。他にも、プロペラ設計やPC内の排熱流れの解析など用途は多いです。単相流は、気体だけでなく液体にも使われます。代表的なのが、パイプ内の流れ解析です。流れを整流させることで、キャビテーション（負圧による気泡の発生）が起こらないパイプ設計が行われます。

混相流というのは、領域が２つ以上の流体で満たされている状態を指します。液体と気体が一般的ですが、水と油のように液体と液体の場合もあります。

こちらは想像しやすいと思います。津波や冷却水など世の中の多くの現象が混相流で起こっており、混相流を正しく解くことが現在のCFD業界では大きな課題となっています。

粒子法

粒子法では、混相流を扱うことになります。なぜかというと、粒子法では粒子のある部分を液体とする代わりに、粒子のない空間を空気として解析するためです。その結果、おのずと混相流となります。

見た目で粒子法と格子法の違いは分かると思いますが、ちゃんと言葉で表すと「計算点が固定か動いているかの違い」とも言えます。

粒子法では、計算点自体が移動します。つまり、実際に流体が移動するわけです。粒子が動いてくれるので、速度や圧力といった値は粒子ごとに与えてあげます。互いの粒子の相互作用によって圧力や速度の値が修正されることで、力が伝わります。

一方で格子法では、固定の計算点で計算をします。計算点は動かずに、流れの速度や圧力といった値を動かすことで、あたかも流体が移動していっているように見えます。具体的には、隣のセルを参照して計算をすることで、隣のセルに値が伝わります。それを何度も繰り返すことで、波の移動が再現できます。

ナビエ・ストークス方程式と物質微分

格子法で使用するナビエ・ストークス方程式は下記のようになります。

$$\frac {\partial v}{\partial t}+(v \cdot \nabla )v=\frac {1}{\rho} \nabla p + { \nu \nabla^2 v}+{g}$$

全部理解する必要はありません。今回注目してほしいのは左辺です。左辺の第一項が非定常項と呼ばれる時間変化の項で、第二項が移流項と呼ばれる流体の移動に関する項です。（補足として右辺も説明しておくと、第一項が圧力項と呼ばれる圧力が流れに影響を与える項、第二項が粘性項と呼ばれる粘性が流れに影響を与える項、最後が重力項です。）

格子法では計算点が固定されており、流体の移動を眺めている形になるので、このような移動に関する項が現れます。

ちなみに粒子法で扱うナビエ・ストークス方程式は下記のようになります。

$$\frac {D v}{D t}=\frac {1}{\rho} \nabla p + { \nu \nabla^2 v}+{g}$$

左辺の$\frac {D v}{D t}$は物質微分（実質微分）と呼ばれ、移動座標系から見た時間変化を示しています。粒子法では計算点が移動するので、それに対応した形で式を書くために物質微分を使用しています。ここで注意してほしいのは、ナビエ・ストークス方程式の形が変わったわけではなく、表示形式の問題と考えてください。