ゼロからはじめる流体力学 超入門」の第三回は流れのある流体について説明します。
前回は静止流体について説明しました。まだ見てないかたは下記からどうぞ。
前回は下記の内容について扱いました。
- 圧力(パスカルの原理)
- 圧力と重力(マノメータ)
- マノメータ
- マノメータによる圧力差測定
- 浮力
流体力学では簡易化した対象に対して計算で流れを解いていくことになります。そのため、前回のように静止していれば簡単に計算ができます。
しかし、動いている場合は少し複雑になるため、環境に制限がかかります。例えばパイプ内やタンクなどに限定された環境でのみ計算が可能となります。
また、時間変化は捉えられないので、定常流れであることも重要です。これらは今回説明します。
定常と非定常
定常とは時間的に変化しない流れを意味します。非定常はその逆で、時間変化するものです。
例えば蛇口から水を出す際は、ある程度の水量だと一定の形で水が出続けますが、あまりにも量が少なかったり多かったりすると水の流れが時々刻々と変わります。
これが定常と非定常の違いです。
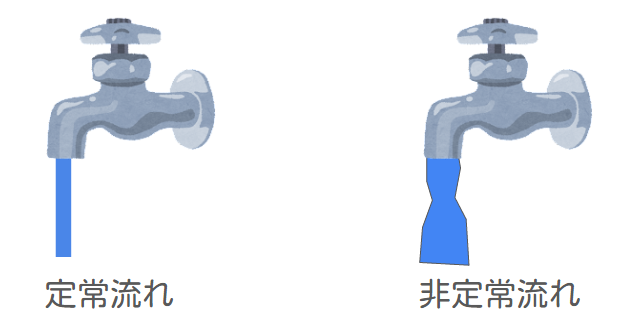
定常流れは非常に安定した流れです。外力がかからない限り、それぞれの場所では同じ流れを観測できます。
流体力学では簡易的なモデルを使いたいため、安定した流れを扱いたいです。そのため、流体力学では定常流れを扱います。
連続の式
ここからは流れの計算に必要な道具を揃えていきます。
まずは連続の式です。非圧縮性流体では、単位体積あたりに出入りする流体の収支が一定になります。

これは直感的にもわかりやすいでしょう。圧縮性のある式だと密度変化がありますが、非圧縮と仮定すると非常に簡単な式になります。
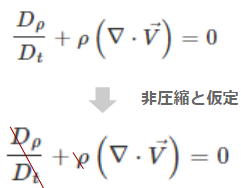
運動量保存則
物理で運動量保存則として、質量と速度の積$mv$が保存されることを学びます。
流体でも同じで、運動量は保存されます。
流体の場合は単位体積あたりで評価するため、質量ではなく流量$Q$と密度$\rho$が使用され、下記のようになります。
$$ \rho Q_1 v_1 = \rho Q_2 v_2 = F $$
これにより、例えば蛇口から出てきた流体とその先に流体などの2点間の運動量保存が表せます。板があって、全ての流体が跳ね返る場合はそこにかかる力Fとも釣り合っていることになります。
もちろん2点間で粘性などの影響がない完全流体であるという条件が必須ですので、制限は忘れないようにしましょう。
エネルギー保存則
CFDでは難しいエネルギー保存則をきちんと扱いますが、流体力学では簡易化した式を使います。それがベルヌーイの定理です。
流体の圧力・位置・流速のエネルギー保存則をベルヌーイの定理と呼びます。
ベルヌーイの定理は簡単な式のため便利ですが、下記の制限があります。
- 定常流れ
- 完全流体(粘性・圧縮性がない)
- 流線に沿った流れ
ベルヌーイの定理は、下記の運動エネルギー・位置エネルギー・圧力によるエネルギーの合計が保存されるというものです。
- 運動エネルギー:$ \frac{1}{2} \rho v^2 $
- 位置エネルギー:$\rho g h$
- 圧力エネルギー:$P$
式が指しているものが少しイメージしにくいですが、これは物理で習ったエネルギー保存式と似ています。
- 固体の運動エネルギー:$ \frac{1}{2} m v^2 $
- 固体の位置エネルギー:$m g h$
- 固体の圧力エネルギー:$P S d$
最後の圧力は「圧力✕面積=力 力✕距離=仕事」という式からエネルギーを求めています。
固体の式に対して、流体は体積で割ったような式となっています。
これは流体が単位体積あたりで評価するため、質量mが密度$\rho$に置き換わったような形となります。
タンクから流出する流速
まずはエネルギー保存則を、タンクの例を使ってみていきましょう。
下記のようなタンクを考えます。
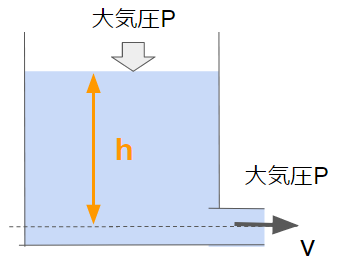
タンクは十分大きく、流出量に比べて水面の減りが十分に小さいこととします。(定常な状態とする)
その場合、エネルギー保存則から下記の式が得られます。(圧力+位置+運動エネルギー=一定)
$$ P + \rho g h = P + \frac{1}{2} \rho v^2$$
両辺の圧力項を消し、流速$v$の式に直すと、タンクの高さから流速が求められます。
$$ v = \sqrt{2 g h} $$
これをトリチェリの定理といいます。
注射器
タンクの例では圧力と位置、運動エネルギー全てを使用しましたが、例えば下記のような注射器の例だと圧力と速度のみで立式できます。
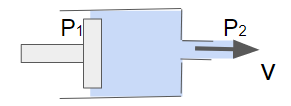
$$ P_1 = P_0 + \frac{1}{2} \rho v^2 $$
$$ v = \sqrt{\frac{2(P_1 – P_2)}{\rho}} $$
ピエゾ水頭
ピエゾ水頭は、エネルギー保存則を用いて流速を求める方法です。
ピエゾ水頭を下記に示します。
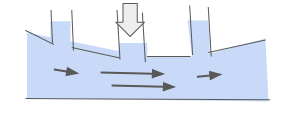
ピエゾ水頭では、圧力一定で管路の流速が高いと相対的に水頭が下がることになります。
これはエネルギー保存則から明らかです。
$$ \frac{1}{2} \rho v^2 + \rho g h + P = const $$
そのため、なかなか観測の難しい流速というパラメータを水頭を評価することで自ずと観測できることになります。
ただし、円管内で流体が円滑に流れており(渦が発生していない)、かつ粘性の影響が無視できる場合に限られることに注意が必要です。
円管流れ
円管は流体力学で非常によく出る問題です。
ここでは連続の式とベルヌーイの定理を両方使う問題について見ていきましょう。
下記のような円管について圧力差や流速を求めたいとします。
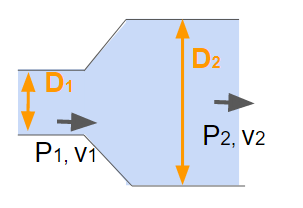
既知の値は下記とします。
- $v_1 = 9 m/s$
- $D_1 = 100 mm$
- $D_2 = 300 mm$
- $\rho = 1000 kg/m^3$
まず、流速$v_2$を求めるために、連続の式を用います。
$$ \rho S_1 v_1 = \rho S_2 v_2$$
面積を直径から求めるようにします。
$$ \rho \frac{\pi}{4} D_1^2 v_1 = \rho \frac{\pi}{4} D_2^2v_2 $$
流速を求める形に直します。
$$ v_2 = \frac{D_1^2}{D_2^2} v_1 = \frac{100 * 10^{-3}}{300 * 10^{-3}} 9 = 1 [m/s]$$
流速が得られたので、次はベルヌーイの定理から圧力差を求めましょう。
$$ \frac{1}{2} \rho v_1^2 + P_1 = \frac{1}{2} \rho v_2^2 + P_2$$
値を代入します。
$$ \frac{1}{2} 1000 * 9^2 + P_1 = \frac{1}{2} 1000 * 1^2+ P_2$$
圧力差を求める形に直します。
$$ P_2 – P_1 = \frac{1}{2} 1000 (9^2 – 1^2) = 40 [kPa] $$
以上により、流速と圧力差を求めることが出来ました。2つの変数がわからない場合は式を2つ用意する必要があることに注意してください。
運動量保存則
ここからは運動量保存則について触れていきましょう。
運動量保存に関して最もわかりやすいのは、蛇口から出る水と板にかかる力が釣り合っている問題です。
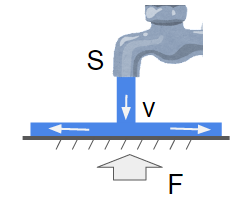
上記の図では板にかかる力$F$と水の運動量が釣り合うので、下記のような式が立てられます。(重力は無視します)
$$ F = -(\rho S v * v)$$
これは「力 = -(流量✕速度)」となっており、運動量の釣り合いを単位体積あたりで表しています。
これを応用して、板が斜めの場合についても考えることが出来ます。
斜めの板における運動量保存
先程は板と蛇口が垂直でしたが、次は傾きのある状態で考えましょう。
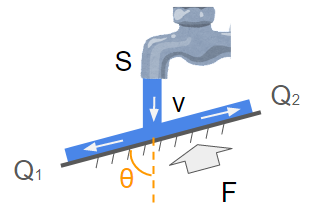
ここで、$F$と$Q_1$、$Q_2$の式を考えてみましょう。
まずは力$F$を得るために、板と蛇口の釣り合いを考えましょう。
$$ F = – (\rho S v * v \sin{\theta}) $$
上記の式は、水道の運動量に対して板に垂直にかかる力を求めています。
質量は変わらないのでそのままで、速度成分を傾きに応じて修正することで垂直にかかる力を得ることが出来ます。
次は流量を求めましょう。
流量は「板に当たる前の運動量 = 当たった後の運動量」という運動量保存則と、連続の式から求めます。
$$ \rho Q v \cos{\theta} = \rho Q_1 v – \rho Q_2 v $$
$$ Q = Q_1 + Q_2$$
これら2つの式から、$Q_1$と$Q_2$が得られます。
$$ Q_1 = \frac{Q(1 + \cos{\theta})}{2}$$
$$ Q_2 = \frac{Q(1 – \cos{\theta})}{2}$$
よって、運動量保存則と連続の式を組み合わせることで、力$F$と流量$Q_1,Q_2$を得ることが出来ました。
ベンチュリ管
最後にベンチュリ管という流量測定装置について扱います。
ベンチュリ管は下記のようになっており、細い部分の流速から流量を測定する装置です。
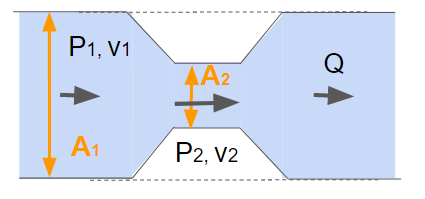
ベンチュリ管では流速$v_2$に関する式を立て、そこから流量$Q$を計算しましょう。
まずはベルヌーイの定理より下記の式が得られます。
$$ P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2 $$
$v_2$の式に直します。
$$ v_2 = \frac{1}{\sqrt{1 – (\frac{A_2}{A_1})^2}} \sqrt{\frac{2(P_1 – P_2)}{\rho}} $$
流速が得られたので、連続の式より流量を求めます。
$$ Q = A_2 v_2 = \frac{A_2}{\sqrt{1 – (\frac{A_2}{A_1})^2}} \sqrt{\frac{2(P_1 – P_2)}{\rho}}$$
上記により流速と流量が得られました。
おわりに
今回は流れを含む流体について計算しました。扱ったのは下記のとおりです。
- 定常と非定常
- 連続の式
- 運動量保存則
- エネルギー保存則
- タンクから流出する流速
- 注射器
- ピエゾ水頭
- 円管流れ
- 運動量保存則
- 斜めの板における運動量保存
- ベンチュリ管
上記のように定常で限定的な状態であれば流体力学が活躍します。
また、連続の式・運動量保存則・エネルギー保存則は流体力学の核となる部分です。CFDとしても重要な考え方なので、ここが理解できるようになるまでじっくり時間をかけて学ぶようにしましょう。
流体力学を使えば、円管や板に噴出する流体などの簡易的な流れは捉えることが出来ます。
CFDをいちいちやるのは結構面倒なので、このような現象の概算として流体力学は非常に役に立ちます。
CFDと並行して流体力学的に値を概算することで、現象理解としても役に立ちます。
現象理解の面から、流体力学を学んでからCFDを行うのは非常に価値があると言えるでしょう。
次回は、やり残した粘性と乱流について扱います。下記からどうぞ。
 ITとCFD入門サイト
ITとCFD入門サイト 

