ゼロからはじめる流体力学　超入門　②静止流体

「ゼロからはじめる流体力学　超入門」の第二回は静止流体について説明します。

流体力学では簡易化した対象に対して計算で流れを解いていくことになります。静止してくれると計算もしやすいので、まずは静止流体を対象とします。

前回は流体の特徴と計算式について説明しました。まだ見てないかたは下記からどうぞ。

前回は下記の内容について扱いました。

• 流体と分子運動
• 大気圧
• 圧縮性
• 粘性（ニュートン流体、非ニュートン流体）
• 流体の方程式

最後に説明した流体の方程式は、今回の静止流体にも大きく関わってきます。

ぜひ前回の説明で全体像を捉えつつ、今回は静止流体という一つの条件について扱っていくことを理解しておくとわかりやすいでしょう。

圧力（パスカルの原理）

非圧縮流体では、全ての面で同じ圧力がかかります。これをパスカルの定理といいます。

• パスカルの定理：流体中ではどこの面でも同じ圧力がかかる

下記の油圧ピストンを考えてみましょう。

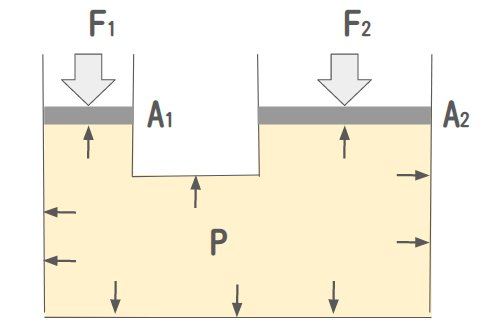
パスカルの定理　と　圧力＝力 / 面積　より、圧力Pは下記の式で表せます。

$$ P = \frac{F_1}{A_1} = \frac{F_2}{A_2} $$

つまり、$F_2$を押すと、小さい力で$F_1$を押し上げることが出来ます。

この原理は油圧シャベルや油圧ブレーキなどに使われています。

圧力と重力（マノメータ）

ここからは圧力と重力の釣り合いについて見ていきましょう。

例えばポンプで水を汲み上げる場合は、強い水圧により水を押し出します。これは水圧により、重力に逆らって高いところまで水を汲み上げています。

ポンプは動きがあるので、流体力学ではマノメータと呼ばれる装置により静止流体の重力と圧力の釣り合いを見ます。

マノメータ

ここでは下記のような液体の入ったマノメータを考えます。

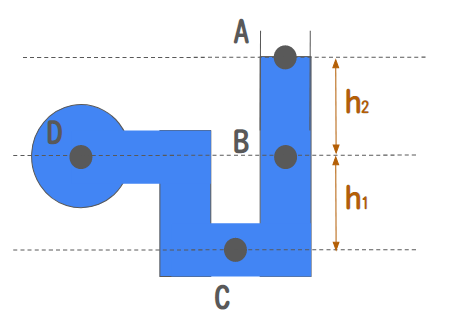
ABCDそれぞれにかかる圧力を考えましょう。マノメータの外は大気圧がかかるものとします。

$$ P_A = (大気圧) $$

$$ P_B = P_A + \rho g h_2 $$

$$ P_C = P_A + \rho g h_2 + \rho g h_1 $$

$$ P_D = P_B = P_A + \rho g h_2 $$

ここで、$\rho$は液体の密度、$g$は重力加速度を表しています。

上記のように、全ての点の圧力は大気圧とその高さ位置から計算することが出来ます。

流体力学において、流体が受ける重力の影響を考えるのは基本となります。

マノメータによる圧力差測定

上記が理解出来たら、マノメータにより圧力差を測る使用例についても見てみましょう。

下記のマノメータを考えます。

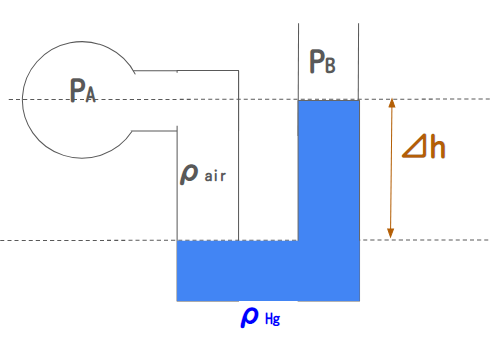
上記のマノメータで外気圧$P_B$と内部圧力$P_A$は下記の式から求められます。

$$ P_A + \rho_{air} g \Delta h = P_B + \rho_{Hg} g \Delta h $$

よって、圧力差$\Delta P$は下記となります。

$$ \Delta P = P_A – P_B = (\rho_{Hg} – \rho_{air}) g \Delta h$$

上記により圧力差が求められたため、内部の圧力をもとに外部圧力を測定できるようになります。

浮力

浮力はアルキメデスの原理が基本となります。

• アルキメデスの原理：浮力は、押しのけた流体に働く重力と大きさが同じで向きが逆となる

例えば下記のような物体の浮力を考えてみましょう。

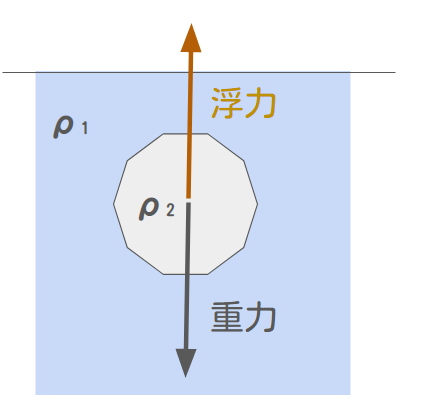
もし物体が静止している場合は、浮力$\rho_1 V g$と重力$\rho_2 V g$が釣り合っていることになります。

$$ \rho_1 V g = \rho_2 V g$$

$V$は物体の体積です。

常識が釣り合っているということは$\rho_1 = \rho_2$であり、流体と固体の密度差がないことになります。

もし固体の密度が高いと沈み、低いと浮きます。水に鉄を入れると沈んで、発泡スチロールを入れると浮くのはこのためです。

固体のほうが密度が小さい場合、水面に浮き出ることで力が釣り合うこともあります。

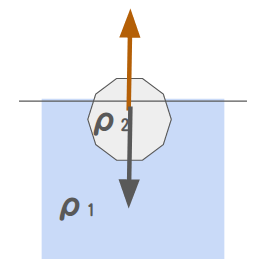
例えば、3割だけ水面に出て釣り合った場合は下記のような式が立てられます。

$$ \rho_1 V g = 0.7 \rho_2 V g$$

つまり、水面に出ている物体の体積から、物体の密度が推定できるということになります。

上記であれば、水面に30%が出ているため、物体の密度は水に比べて$\frac{7}{10}$であることがわかります。

おわりに

今回は流体力学の中でも静止流体について扱いました。触れた内容は下記のとおりです。

• 圧力（パスカルの原理）
• 圧力と重力（マノメータ）
• マノメータ
• マノメータによる圧力差測定
• 浮力

静止流体においては圧力が非常に重要です。

今後、流れが発生しても圧力は切っても切れない関係になってきます。

特に流体を非圧縮で考える場合は、CFDにおいても圧力を慎重に判断する必要があります。ぜひ今回の内容で感覚をつかんでください。

次回は流れを含む流体について扱います。