ゼロからはじめる流体力学超入門 ④粘性と乱流【レイノルズ数】

ゼロからはじめる流体力学　超入門」の第三回は流れのある流体について説明します。

前回は流れる流体について説明しました。まだ見てないかたは下記からどうぞ。

ゼロからはじめる流体力学　超入門　③流れ【連続の式とエネルギー保存】

前回は下記の内容について扱いました。

定常と非定常
連続の式
運動量保存則
エネルギー保存則
タンクから流出する流速
注射器
ピエゾ水頭
円管流れ
運動量保存則
斜めの板における運動量保存
ベンチュリ管

流体力学では簡易化した対象に対して計算で流れを解いていくことになります。しかし、動いている場合は少し複雑になるため、環境に制限がかかります。例えばパイプ内やタンクなどに限定された環境でのみ計算が可能となります。

また、簡易化のために、定常流れかつ非粘性を対象として計算ました。

今回は今まで無視してきた粘性と乱流について説明します。

粘性

粘性は流体の特性の一つです。

流体力学では簡易化しないと手計算できないものについては扱わないため、流れを複雑化する粘性を考慮することはありませんでした。

ただ、粘性は流れに対して非常に大きな影響を与える要素です。そこで、ここでは粘性の特性について見ていきましょう。

流れを支配するナビエ・ストークス方程式を下記に示します。

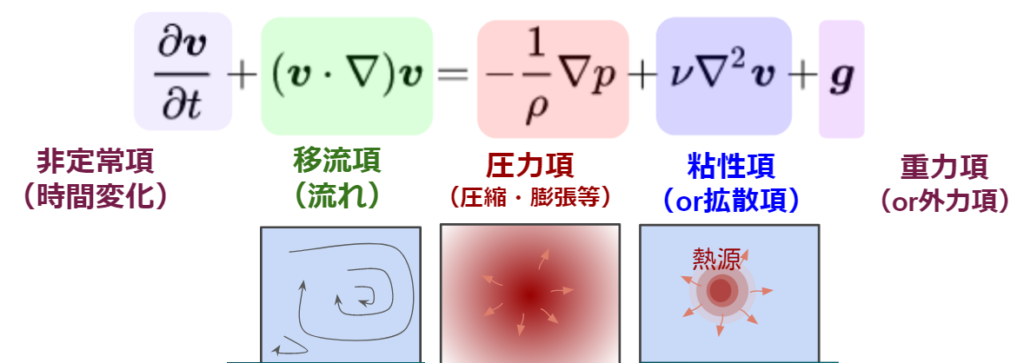
粘性項が右辺にあるのがわかるように、粘性は流体特性の中でも重要な要素であることがわかると思います。

直感的な理解としては、粘性は周りの流れを巻き込みます。例えば、局所的な流れがあった場合は、時間とともに周りと平滑化した流れになってきて遅い部分と早い部分の境目がなくなります。

ここでは、定常で非常に簡単な流れを対象に計算を行い、粘性について直感的に理解しましょう。

クウェット流れ

クウェット流れとは、２平面間の流れにおいて片方の面が静止しておりもう一つが動いているような流れのことです。

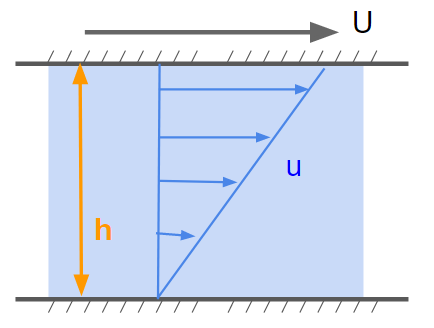
クウェット流れでは、２面間に速度勾配が生まれます。

２面感の速度は下記で表すことが出来ます。

$$ u = \frac{U}{h} y $$

$y$は高さ方向の座標です。この式を見てみると、$y = h$で最大となり、$y = 0$で速度ゼロとなります。

ポアゾイユ流れ

ポアゾイユ流れは、２面間の流れにおいて入口に流速を与えて、その流速が壁面により抑制されるような流れのことです。

壁面速度がゼロで中央部では流速を維持しようとするため、粘性の影響でこのような流速勾配が生まれます。

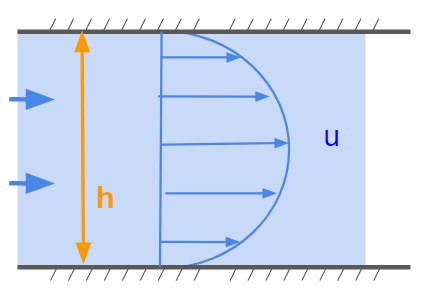
ポアゾイユ流れの流速は下記で表せます。

$$ u = \frac{\Delta P}{2 \mu} (hy – y^2) $$

$y$は高さ方向の座標です。この式を見てみると、流速$u$は$y = \frac{1}{2} h$で最大となり、$y = 0,h$で速度ゼロとなります。

壁面による流速の低下は多くの例で現れます。この例は非常に簡易的ですが、CFDなどで得られた結果の検証としても参考となるため、覚えておくと良いでしょう。

乱流

流体力学では安定した流れである層流を対象としますが、流体には乱れた流れの乱流もあります。

乱流では時々刻々と流れが変化し、流れが一意の状態に定まりません。例えば、急な流れの中に何か物体を置くと、乱流が発生します。

乱流の指標としてよく使われるのがレイノルズ数です。レイノルズ数が大きいと渦が発生します。

レイノルズ数は下記の式で定義されます。

$$ Re = \frac{慣性力}{粘性力} = \frac{\rho U L}{\mu} = \frac{U L}{ \nu} $$

ここで$U$ は代表速度、$L$は代表長さ、$\mu$は粘度、$\nu$は動粘度です。

この式から、下記のようなことが言えます。

小さい領域＆粘性が高い　→　Re大
大きい領域＆粘性が低い　→　Re小

空気などの低粘度な流体中で、急激な流れの中にある物体は乱流が発生しやすくなります。一方で、はちみつや樹脂などの高粘度な流体は、レイノルズ数が低いので乱流について考える必要がありません。

レイノルズ相似則

また、レイノルズ数が等しい流体では同じ流れになるという法則があります。これをレイノルズ相似則といいます。

レイノルズ相似則：レイノルズ数が同じだと同じ流れになる

これを活かすことで、大きな装置の流れを小型の実験で模擬することが出来ます。

例えば、ジェット機の設計などで活用されています。

ナビエ・ストークス方程式

ナビエ・ストークス方程式を無次元化する際に、レイノルズ数が使用されます。

ナビエ・ストークス方程式を無次元化した式は下記のようになります。

$$ \frac{\partial u’}{\partial t’} + u’ \frac{\partial u’}{\partial x’} + v’ \frac{\partial v’}{\partial y’} = – \frac{\partial p’}{\partial x’} + \frac{1}{Re} ( \frac{\partial^2 u’}{\partial x’^2} + \frac{\partial^2 u’}{\partial y’^2}) – \frac{g L}{U^2} $$

ここで、各変数の定義は下記のようになります。

$$x’ = \frac{x}{L} , y’ = \frac{y}{L} $$

$$u’ = \frac{u}{U} , v’ = \frac{v}{U} $$

$$t’ = \frac{t}{\frac{L}{U}} $$

$$ p’ = \frac{p}{\rho U^2}$$

無次元のナビエ・ストークス方程式は、主に数値計算の結果の検証に使われます。

CFDでは流れが重要であるため、レイノルズ数を揃えて結果が妥当であるかを確認することになります。CFDを扱う場合は、論文などで良くレイノルズ数が使われるので、定義を覚えておきましょう。