今回は差分法・有限要素法・粒子法の特徴について説明します。
全て数値計算でよく利用されるものであり、流体解析や構造解析に利用されています。
同じ対象を計算する場合でも、手法によって大きく結果が異なる場合があります。それは、数値計算が完璧でないところに原因があります。
これらの手法はそれぞれ一長一短であり、解析したい現象がそれぞれの手法の短所に当たってしまうと、上手く現象を捉えきれない場合があります。
特に重要なのはそれぞれの特徴と長所を理解することです。
今回の内容により特徴を理解し、解析手法の使い分けを行えるようになりましょう。
差分法
有限差分法(Finite Difference Method)は空間を離散化する手法です。離散化とは、連続的な空間をメッシュで区切って分割し、コンピュータで小分けにして計算できるようにすることです。
例えば、世の中の流体や個体は連続的な物体ですが、これらを細かいセルに区切ることで単純化した領域として計算することができるようになります。
一般的に離散化では、直交した等間隔の格子が用いられます。
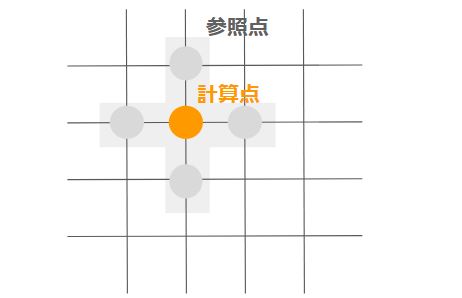
差分法では周囲の点から計算点の計算を行います。
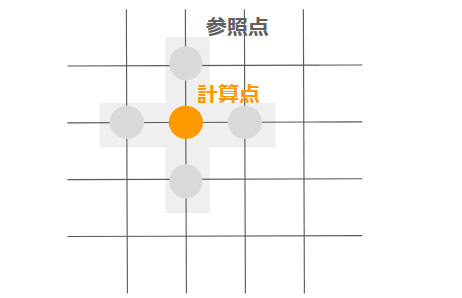
式で書くと下記のようになります。
$$ \phi_{ij} = \frac{ \phi_{i-1,j} + \phi_{i,j-1} + \phi_{i+1,j} + \phi_{i,j+1} }{ 4 \Delta x } $$
ここで、$\phi$は任意の物性であり、下付き文字のiとjは格子のx軸とy軸の位置を指しています。
つまり、周囲の4点から計算するという手法が差分法の基礎となります。
応用として、不等間隔格子や円筒座標系が使われることもあります。また、差分法は空間だけでなく、時間の離散化にも利用されます。
差分法は他の手法の基礎となる手法です。たとえ空間離散化が有限要素法や粒子法であっても時間は差分法を使います。
そのため、遠回りでもまずは差分法から学ぶと理解しやすいでしょう。
有限要素法
有限要素法(Finite Element Method)では、差分法と異なり移動可能なラグランジュ格子を用います。
(固定された格子はオイラー格子、移動可能な格子はラグランジュ格子と呼ばれます)
また、有限要素法のもう一つの特徴は、内挿近似です。
内挿近似はその名の通り、周囲の点から内部の値を推定することです。
有限要素法では、各点に対して定義される形状関数と呼ばれる関数があり、これを用いてひずみと応力の関係などを計算します。
形状関数は自分の節点で1、他の節点で0となるように定義されており、なめらかに1から0に変化するように設定されています。
これにより、形状関数を用いて内挿近似が可能になります。
例えば、3点(a1, a2, a3)の勾配を計算するなら、各点の値($\phi_1, \phi_2, \phi_3$)と形状関数Nの勾配を用いて下記でかけます。
$$ \nabla \phi (x_1, x_2) = \phi_1 \nabla N_1 (x_1, x_2) + \phi_2 \nabla N_2 (x_1, x_2) + \phi_3 \nabla N_3 (x_1, x_2) $$
粒子法
粒子法は、原子の動きを捉える手法である分子動力学から発展した手法です。分子というミクロな対象を解析する手法をマクロに応用することで、マクロ的な流れを解析できるようになりました。
粒子法は大きく分けて2種類あり、SPH法とMPS法が挙げられます。
これらは流体などの連続体を粒子で粗視化して運動を捉える手法です。
DEM(離散要素法)も粒子ですが、粉体などの離散的な対象を扱うことが多いため、離散化する過程がない点で、粒子法としてくくられない場合が多いです。
ここからは粒子法であるSPH法とMPS法について説明していきます。
SPH(Smoothed Particle Hydrodynamics)は元々天体物理学に用いられた手法でしたが、圧縮性流体の解法として用いられるようになりました。
その後は非圧縮性流体や固体の解析にまで応用されています。
SPH法はカーネル関数と呼ばれる1つの粒子の周囲への影響の重みを表した関数であり、粒子と直接接触していない場合でも周囲に影響を与えられるのが特徴です。
このカーネル関数を微分することで、ナビエ・ストークス方程式の勾配やラプラシアンの近似モデルが作られます。
一方で、MPS法(Moving Particle Semi-implicit)は、非圧縮性流体を対象とした手法であり、その名の通り半陰解法で解くのが特徴です。
半陰解法とは、速度は陽的(過去の時間をもとに現在時刻を計算)で、圧力は陰的(現在の時間をもとに現在時刻を計算)に計算する手法です。
非圧縮性流体では圧力振動が発生しやすいため、安定しやすい陰解法が使われています。
重み関数も、連続関数の近似ではなくテイラー展開により微分の近似を行います。そのため、式の導出や形の見た目が大きく異なります。
ただし、結果的にはどちらも安定的な微圧縮の計算に向かっており、2つの手法の解析結果の差は小さくなっています。
おわりに
今回は3つの計算手法である差分法・有限要素法・粒子法について紹介しました。
それぞれの特徴は下記のとおりです。
- 差分法は等間隔格子から周囲の参照点の情報より計算点の値を求める手法
- 有限要素法は、動く格子から内挿近似により計算点を求める手法
- 粒子法は影響半径内にある周囲の粒子との相互作用により粒子の値を求める手法
同じように連続体の離散化に使われますが、大きく異なる手法であることがわかると思います。
これらの特徴より、例えば粒子法は大移動の計算が得意だとか、格子法は隙間がないので圧力計算が得意だとかといった長所もわかってきます。
それぞれの手法の特徴を理解して、上手く使い分けるようにしましょう。
 ITとCFD入門サイト
ITとCFD入門サイト