【CFD/格子法】CLSVOF法について【二相流】

CLSVOF法とは、Coupled LevelSet Volume Of Fraction methodの略です。二相流解析で液面を取得したいときに使います。

CLSVOF法は、LevelSet法とVOF法を組み合わせた手法なので、まずはそれぞれの手法について理解しましょう。

VOF法

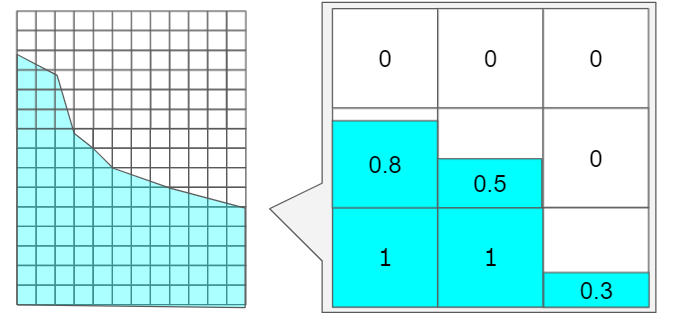
VOF法は「体積分率」と呼ばれる値を移流させることで、どのくらい液体に満たされたセルであるかを判断します。

体積分率（VOF値）は0~1の範囲であり、0が気相、1が液相であることが一般的です。VOF値が0.5の位置を界面とします。

VOF法は非常にシンプルな手法なので、入門に最適です。VOF法をカスタマイズして高精度化する手法も多く提案されており、結構性能も良いので、多くのソフトウェアで使用されています。

VOF法のデメリットとしては、界面がぼやけてしまうことです。格子法における移流計算は誤差が出やすいため、VOF法も例に漏れず誤差が出やすいです。

移流計算を安定させるためには数値拡散を与える必要があり、数値拡散により界面形状の精度を悪化させてしまいます。

LevelSet法

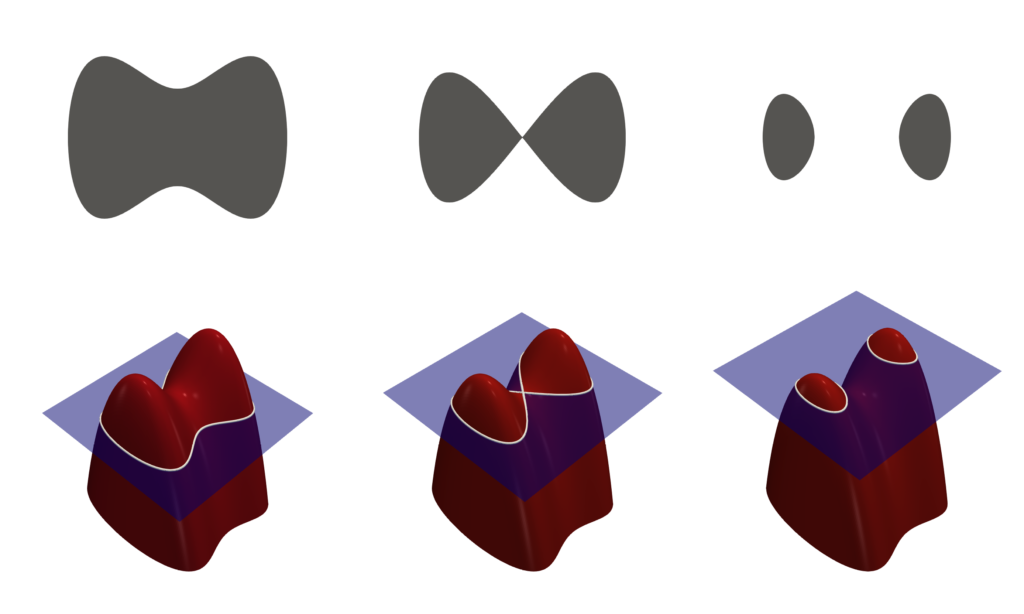
レベルセット法は、界面をゼロとする「符号付き距離関数」を使うことで、界面を捉える手法です。

符号付き距離関数は、界面を基準の$\phi = 0$とします。そして、界面からの接線方向の距離に応じて、液相側はプラス、奇想側はマイナスの値が割り振られます。

法線方向距離に基づいた界面であるため、法線方向に圧縮をかけてぼやけを解消することも可能です。これがレベルセット法特有の「再初期化」のステップに当たります。

レベルセット法は、界面をシャープに捉えられるのが大きなメリットです。

一方で、レベルセット法のデメリットとしては、保存性の悪さが挙げられます。VOF法に比べると、小さな気泡や液滴が消えやすいという問題があります。

CLSVOF法

CLSVOF法はレベルセット法とVOF法の２つを組み合わせた手法です。

それぞれの欠点を補うため、VOF法で界面を捉え、レベルセット法で幾何計算をします。

計算量は増えますが、界面の取得方法としてはトップクラスの精度があります。

ここでは、レベルセット法の移流計算を行わない「S-CLSVOF法」について紹介します。

S-CLSVOF法

基本のCLSVOF法は、VOFとレベルセット両方の計算を行います。一方で、S－CLSVOF法ではVOFのみ移流計算を行うため、計算量が少ないという特徴があります。

つまり、VOFで液相の移流を計算し、レベルセットで界面の修正と幾何計算を行うという流れになります。

手順としては、下記の通りです。

１．体積分率$\alpha$の移流
２．体積分率 $\alpha$ から、符号付き距離関数の初期値$\phi_0$の計算
３．符号付き距離関数$\phi$の再初期化
４．物性値$\rho , \mu$の計算
５．界面の幾何計算

１．体積分率$\alpha$の移流

まずは、体積分率$\alpha$の移流を行います。ここは普通のVOF法と同じです。

$$ \frac{\partial \alpha}{ \partial t} + \nabla \cdot (\alpha v) = 0 $$

特殊な方法として、移流計算の拡散を抑えるための「逆拡散項」を与えることもあります。

$$ \frac{\partial}{ \partial t} (\rho \alpha) + \nabla \cdot (\rho \alpha v) + C_{ad} \nabla \cdot (\alpha (1 – \alpha) v_a)= 0 $$

両辺に密度$\rho$がかかっていることに注意してください。

第３項が逆拡散光であり、$C_{ad}$は逆拡散係数、$v_a$は人工圧縮速度です。

２．体積分率 $\alpha$ から、符号付き距離関数の初期値$\phi_0$の計算

次に、体積分率に合わせて符号付き距離関数を作成します。

体積分率では界面が$\alpha = 0.5$の位置にあるのに対し、符号付き距離関数では界面が$\phi = 0$の位置にあるため、そのまま代入はできません。

よって、下記の式で変換します。

$$ \phi_0 = (2 \alpha – 1) \Gamma $$

$\Gamma$は無次元量であり、セルの大きさに基づいて決定されます。例えば、$\Gamma = 0.75 \Delta x$などです。

３．符号付き距離関数$\phi$の再初期化

次は、符号付き距離関数$\phi$の再初期化を行います。

再初期化は、界面からの距離に応じて符号付き距離関数を再定義することで、界面を鮮明にします。

再初期化は下記の式で行われます。

$$ \frac{\partial \phi }{\partial \tau} = sign(\phi) (1 – | \nabla \phi |) $$

$\tau$ は人工タイムステップであり、$ \Delta tau = 0.1 \Delta x$程度を使用します。

$sign(\phi)$は、$\phi$の符号（＋ー）を取得します。

常識は、$\phi = 0$である界面位置は動かさず、$\phi$の値のみを修正しています。

上記の再初期化は、界面の幅に応じた繰り返し計算が必要になります。反復数は、$ \frac{\epsilon}{\Delta t} $で得られます、

ここで、$\epsilon$は界面幅で$\epsilon = 1.5 \Delta x$、$\Delta \tau$は反復計算で使用する人工タイムステップです。

４．物性値$\rho , \mu$の計算

得られた符号付き距離関数から、密度や粘度を計算します。

密度$\rho$と粘度$\mu$は符号付き距離関数を使って、下記の式で得られます。

$$ \rho = He(\phi) \rho_1 + (1 – He(\phi)) \rho_2 $$

$$ \mu = He(\phi) \mu_1 + (1 – He(\phi)) \mu_2 $$

下付き文字の1と2は、２つの相のそれぞれの物性値を表しています。

$He$はヘビサイト関数で、0から1を滑らかにつなぐ関数です。

$$He =
\begin{cases}
0 & (\phi < – \epsilon) \\
\frac{\phi + \epsilon}{ 2 \epsilon} + \frac{sin(\frac{\pi \phi}{ \epsilon })}{2 \pi} & (| \phi | \leq \epsilon) \\
1 & (\phi > \epsilon)
\end{cases}$$

ここで \epsilon は界面幅であり、 $\epsilon = 1.5 \Delta x$程度を使います。

５．界面の幾何計算

最後に、曲率から表面力計算を行います。

曲率は下記で得られます。

$$ \kappa (\phi) = – \nabla \cdot \frac{\nabla \phi}{ | \nabla \phi | } $$

プログラム上では、ゼロ割を防ぐために分母に微小な値を足してください。

曲率を使用すると、表面力は下記の式で得られます。

$$ F = \sigma \kappa_{\phi} \delta_{\phi} \nabla \phi $$

$sigma$は表面張力係数、$kappa_{\phi}$は曲率、$delta_{\phi}$はディラックのデルタ関数です。

ディラックのデルタ関数 $delta_{\phi}$ は下記の式で得られます。

$$ delta_{\phi} =
\begin{cases}
\frac{1}{2 \epsilon} ( 1 + cos(\frac{\pi \phi}{\epsilon}) ) & (| \phi | \leq \epsilon) \\
0 & (| \phi | > \epsilon)
\end{cases}$$

繰り返しになりますが、$\epsilon$は界面幅です。

つまり、ディラックのデルタ関数は、界面幅以上の部分では表面力が働かないということを意味しています。