【CFD/Python】二次風上差分とQUICK【CFDプログラミング講座 #5 移流項編】

この講座ではPythonを使用したCFDプログラミングを解説していきます。最後まで受講して頂くと、差分法による流体解析ができるようになるようにしています。ぜひ最後までお付き合いください。

第２回からは移流項に関する解説をしていきます。移流項は最も難しい部分ですが、特に重要なので先に解説します。

前回の第４回では移流方程式の離散化スキームであるLax-Wendroff法について解説しました。まだ見てない方は下記からどうぞ。

【CFD/Python】Lax-Wendroff法【CFDプログラミング講座　#4　移流項編】

重要な項目は下記の通りです。 Lax-Wendroff法は中心差分に対して２次の拡散を加えることで安定性を補った手法です。ただし、結果としてはまだ数値振動が発生してしまいました。

Lax-Wendroff法は二次多項式を使う手法である
二次多項式を使うことで、精度を維持したまま人工粘性を与えられる
Lax-Wendroff法は中心差分に二次の粘性を加えることで、精度と安定性を両立する
高次多項式はLax-Wendroff法の考え方の延長である

二次精度風上差分

ここでは二次精度風上差分について説明します。

一次精度風上差分

まずは、先に一次精度の風上差分について振り返りましょう。今まで風上差分とよんでいたのが、一次の風上差分です。

一次風上差分は、計算点とその一つ風上側の点を参照する方法でした。

\frac {\partial v} {\partial x} \approx c \frac{v_{i}-v_{i-1}}{\Delta x} $$

特に右辺の分子に注目してください。中心差分ではi点の両端を使用していましたが、風上差分ではi点とi-1点という隣り合った値を使用します。隣り合った値を参照することで、格子幅の大きさの波まで捉えることができるので振動が起きにくくなります。

風上差分は安定性は高い一方で、人工粘性が入っているぶん精度は下がるという特徴がありました。

二次精度風上差分

二次（精度）風上差分は、一次風上差分の参照点を増やすことで精度を上げる手法です。一次だと参照点が２つなのに対し、二次風上差分は参照点が３つになります。

図で説明します。下記の図を見てください。

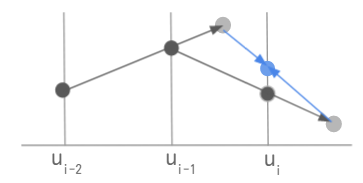
青で示しているのが、計算点 $ u_i $ です。そして、濃い黒が参照点です。３つの黒い参照点を二段階の計算を通して、最終的に青い点を計算します。

ポイントは、 $ u_{i-2} $ と $ u_{i-1} $ を使って $ u_{i – \frac{1}{2}} $ を計算し、 $ u_{i-1} $ と $ u_{i} $ を使って $ u_{i + \frac{1}{2}} $ を計算しているところです。最終的に、 $ u_{i – \frac{1}{2}} $ と $ u_{i + \frac{1}{2}} $ を使って $ u_i$ を計算しています。

つまり、一次風上差分は２つの節点の値を使っていたのに対し、二次風上差分は３つの節点を使うことで実質は節点間の値を使っているということです。従来は節点の解像度で計算していたものが、節点の２倍の解像度で扱えるようになることで精度が上がったというわけです。

最終的に節点間の値を参照することで精度を上げるというのは、後述のQUICK法も同じです。

その結果、得られる式は下記のようになります。

$$ u^{n+1} = u_i – c \fanc{\Delta t}{2 \Delta x} (3 u_i – 4 u_{i-1} + u_{i-2}) $$

計算としてやっていることは非常に単純で、計算点 $ u_i $ と２つ隣の計算点 $ u_{i-2}$を使って、テイラー展開をすると得られます。ここでは詳細の説明は初略しますが、調べると簡単に理解できると思います。

QUICK法

次はQUICK法です。QUICKは、Quadratic Upstream Interpolation for Convective Kinematics（直訳すると、対流運動学のための二次上流補完）の略です。

QUICKも二次風上差分とイメージは同じです。二次風上では２点を使用して $ u_{i + \func{1}{2}} $ 点と $ u_{i – \func{1}{2}} $ 点を求めましたが、QUICK法では３点を使用して $ u_{i + \func{1}{2}} $ 点と $ u_{i – \func{1}{2}} $ 点を求めます。

QUICK法はその結果、４つの参照点を使用することになります。具体的には、計算点に対して風上側に２点と風下側の１点を追加した４点を使用して計算します。

下記に計算手順の図を示します。

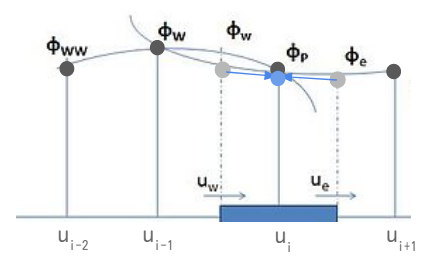
黒い点を参照して灰色の $ u_{i + \func{1}{2}} $ 点と $ u_{i – \func{1}{2}} $ 点を計算します。そして、その２点から青い点を計算する手順になります。

特に意識してほしいのは、３点を補完に使用することで曲線的に $ u_{i + \func{1}{2}} $ 点と $ u_{i – \func{1}{2}} $ 点の補完ができていることです。線形補完だった二次風上よりも精度が良さそうなのが体感的にわかると思います。

その結果、得られる式は下記のようになります。

$$ u^{n+1} = u_i – c \fanc{\Delta t}{8 \Delta x} ( 3 u_{i+1} + 3 u_i – 7 u_{i-1} + u_{i-2}) $$

参照点を増やすことで、かなり良い補完ができそうなことがわかりました。ここからは実際の精度と安定性を評価するために、プログラムの作成に移っていきましょう。

二次元風上プログラム

二次風上を使ったコードは下記の通りです。

#二次風上
import numpy 
import matplotlib.pyplot as plt
%matplotlib inline


nx = 501
dx = 2 / (nx - 1)
nt = 1000 
dt = .0005 
c = 1

u = numpy.zeros(nx) 
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1  

for n in range(nt):  
    
    u_old = u.copy() 
    u[2:-2] = u_old[2:-2] - c * dt / ( 2 * dx) * (3 * u_old[2:-2] - 4 * u_old[1:-3] + u_old[:-4]) 
    
    if n % 200 == 0:
        plt.plot(numpy.linspace(0, 2, nx), u)

plt.show()

出力結果は下記のようになります。

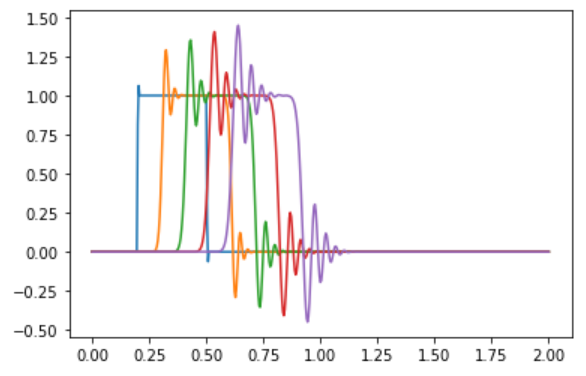
二次元差分を使っても、振動は出てしまっています。一次の風上差分よりは滑らかさが少なくて矩形に近いですが、振動が出てしまっているのを見ると、まだ実用的ではない印象がありますね。

ライブラリ

上から順にプログラムを解説していきます。まずは使用するライブラリのインポートからです。

import numpy 
import matplotlib.pyplot as plt
%matplotlib inline

使うライブラリはnumpyとmatplotlibです。import 〇〇と書くことでライブラリをインポートでき、as〇〇と書くことで別名を定義できます。

numpyは配列演算に関するライブラリです。まとめてデータを扱えて計算が高速であることから、数値計算では非常によく使われます。npという省略表記されることも多いです。

pythonにはリストという機能がありますが、今回はnumpyを使用します。numpyでは格納される型が揃っており、他のライブラリとの相性の面でも使い勝手がよいです。

matplotlibはグラフ描画用ライブラリです。計算結果を可視化するために使用します。

今回はmatplotlib内のpylotというメソッドを多用するので、pltという省略名で定義しておきます。これによってplt.〇〇という表記で使用することができ、プログラムがスッキリします。

初期化

ここでは解析の初期条件を与えます。

初期条件として、格子数や時間刻み幅などのパラメータから、どこにどのくらいの速度を与えるかまで決定してやる必要があります。

nx = 501
dx = 2 / (nx - 1)
nt = 1000 
dt = .0005 
c = 1

u = numpy.zeros(nx) 
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1

nxは格子の節点数です。nxは節点なのでセル数はnx-1個になることは注意してください。今回から説明する差分法では計算点が節点になります。そのため、501点の計算点があると考えてください。

dxは接点間距離です。セルの大きさと言い換えてもらっても良いです。

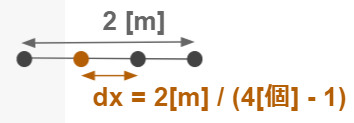
今回は計算領域の長さを２ｍとするため、このような式となっています。複雑そうに見える場合は下記の節点が少ない場合の例を表した図を見ると、わかりやすいと思います。

節点が両端に位置することになるので、接点間距離はnx-1個の間隔で割ることがわかります。

ntはステップ数です。今回はforループで時間を進めるので、1000回ループ計算を行うことになります。言い換えると、1000回も移流方程式を解くことになります。

dtは時間刻み幅です。１回のステップで進む時間を表します。CFDでは時間刻み幅は非常に重要な要素です。計算の安定化のために調節してやる必要があります。

cは流速（速度）です。線形移流方程式なので、流速は定数になります。

uは輸送される任意の変数です。ナビエ・ストークス方程式なら流速、熱やVOF値の場合もあります。初期値として、0.2~0.5の範囲で1を与えてやります。他は0に設定しているので、 0.2~0.5の範囲だけ1となる矩形波が現れます。

移流方程式（二次風上差分法）

ここからがメインの計算ループになります。

今回は矩形波を時間経過とともに右側に流すプログラムになるので、時間をforループで進めます。

for n in range(nt):  
    
    u_old = u.copy() 
    u[2:-2] = u_old[2:-2] - c * dt / ( 2 * dx) * (3 * u_old[2:-2] - 4 * u_old[1:-3] + u_old[:-4]) 
    
    ・・・

nステップを0~ ntまで変化させて時間変化を計算します。forループ内に移流方程式が入ります。

u_oldは古い時間ステップにおける輸送変数uの値です。uの値は移流方程式で更新されるため、u_oldを右辺において新しい値はuに代入することとします。

pythonでは配列をまとめて演算するのでこのような一時変数は不要ですが、他の言語にも対応できるように一般的な書き方をしています。

次の行は、移流方程式を二次風上差分法で書いた式です。下記の式をプログラム化しています。

$ u^{n+1} = u_i – c \fanc{\Delta t}{2 \Delta x} (3 u_i – 4 u_{i-1} + u_{i-2}) $$

配列の範囲が2:-2となっているのは、領域の両端の２つの節点では移流方程式を計算していないからです。両端の２つの節点は参照点としてだけ使用します。二次風上は２つ左隣りの点まで参照するので、[2:-2]となっています。

これは、移流方程式を風上差分で離散化した際に、計算点の隣の節点を参照するためです。そのため、端の計算点は計算出来ないことになります。

（厳密には風上側の端２点が計算できません。プログラムをわかりやすくするために両端の節点を計算から外しています）

離散化スキームの変更には、この１行を変更すれば良いことがわかります。

グラフ描画

グラフ描画には、初めにインポートしたグラフ描画ライブラリのmatplotlibを使用します。

for n in range(nt):  
    ・・・            
    
    if n % 200 == 0:
        plt.plot(numpy.linspace(0, 2, nx), u)

plt.show()

for文の中にif文があります。ここで、時間ステップが200進むごとに画面出力をしています。

plt.plotはグラフの描画を行います。横軸と縦軸を指定することでグラフを描画できます。

横軸はnumpy.linspaceを使用します。linspaceは指定した範囲を等間隔で分割した配列を作成してくれます。ここでは横軸には0~2までをnx分割し、縦軸はuを使用することにより、縦横で同じ要素数の配列を作成できます。

最後のplt.showはグラフの画面表示です。plotは描画に対してshowは表示です。plotでグラフを重ねて描画し、showでまとめて表示しています。

結果として下記のようなグラフが出力されます。

QUICK法のプログラム

QUICKを使用したコードは下記の通りです。

#QUICK 「次数が増える」と安定性は関係なし
import numpy 
import matplotlib.pyplot as plt
%matplotlib inline


nx = 501
dx = 2 / (nx - 1)
nt = 1000 
dt = .0005 
c = 1

u = numpy.zeros(nx) 
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1  

for n in range(nt):  
    
    u_old = u.copy() 
    u[2:-2] = u_old[2:-2] - c * dt / ( 8 * dx) * (3 * u_old[3:-1] + 3 * u_old[2:-2] - 7 * u_old[1:-3] + u_old[:-4]) 
    
    if n % 200 == 0:
        plt.plot(numpy.linspace(0, 2, nx), u)

plt.show()

出力結果は下記のようになります。

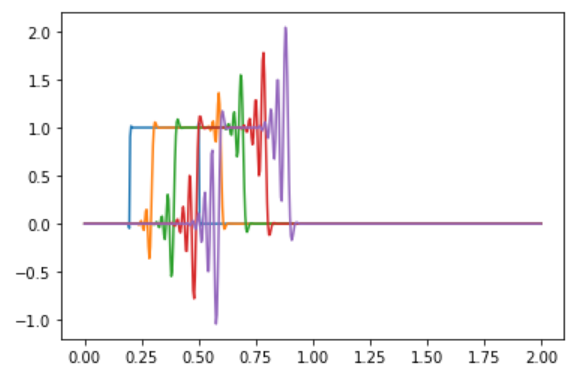
二次風上だと矩形波の上の角が振動していると同時に逆側が滑らかになっていました。しかし、QUICKだと振動は発生しているものの波は滑らかになっていません。

どちらも振動が大きいために、小さな違いに思えるかもしれません。しかし、このように振動の大きさと滑らかさにそれぞれ強い手法を知っておくことで適切にスキームを選択することができるようになります。

ただ、一つ一つを覚えておく必要はありません。ひとまずここでは、項を増やして補完を工夫しても、振動を防ぐのは非常に難しいということを覚えておきましょう。

移流方程式（QUICK法）

ここからがメインの計算ループになります。

今回は矩形波を時間経過とともに右側に流すプログラムになるので、時間をforループで進めます。

for n in range(nt):  
    
    u_old = u.copy() 
    u[2:-2] = u_old[2:-2] - c * dt / ( 8 * dx) * (3 * u_old[3:-1] + 3 * u_old[2:-2] - 7 * u_old[1:-3] + u_old[:-4]) 
   
    ・・・

nステップを0~ ntまで変化させて時間変化を計算します。forループ内に移流方程式が入ります。

pythonでは配列をまとめて演算するのでこのような一時変数は不要ですが、他の言語にも対応できるように一般的な書き方をしています。

次の行は、移流方程式をQUICK法で書いた式です。下記の式をプログラム化しています。

$ u^{n+1 $$ u^{n+1} = u_i – c \fanc{\Delta t}{8 \Delta x} ( 3 u_{i+1} + 3 u_i – 7 u_{i-1} + u_{i-2}) $$

配列の範囲が2:-2となっているのは、領域の両端の２つの節点では移流方程式を計算していないからです。両端の２つの節点は参照点としてだけ使用します。QUICK法は２つ左隣りの点まで参照するので、[2:-2]となっています。

これは、移流方程式をQUICK法で離散化した際に、計算点の隣の節点を参照するためです。そのため、端の計算点は計算出来ないことになります。

（厳密には風上側の端２点と風下側の端１点が計算できません。プログラムをわかりやすくするために両端の節点を同じ数だけ計算から外しています）

また、注目してほしいのは、二次風上差分でもQUICK法でも更新後の変数の範囲が[2:-2]となっていることです。

どちらも流れの方向に応じて参照点を変える必要があるので、実質は風上風下の両側を参照点として取れるようにしておく必要があります。

風上風下どちらも確保しておくのであれば、有効活用できたほうが良いです。ということはつまり、QUICK法を使えば二次風上差分とほぼ同じ労力で精度をあげられるということになります。

QUICK法という大それた名前ですが、それにふさわしい便利さがあることがわかっていただけたでしょうか？