この講座ではPythonを使用したCFDプログラミングを解説していきます。最後まで受講して頂くと、差分法による流体解析ができるようになるようにしています。ぜひ最後までお付き合いください。
第二回からは移流項に関する解説をしていきます。移流項は最も難しい部分ですが、特に重要なので先に解説します。
前回の第2回では移流方程式について解説しました。まだ見てない方は下記からどうぞ。
重要な項目は下記の通りです。これから移流項について解説しますが、風上差分と中心差分が中心となります。まずはこの2つを抑えましょう。
- 移流項は流体の流れを支配する項である
- 移流方程式は非定常項と移流項だけでできている
- 移流項の離散化においては、精度と安定性のバランスが重要である
- 中心差分は精度は高いが安定性が低い
- 風上差分は精度は低いが安定性が高い
- 高度な離散化手法を使うことで、精度と安定性を両立させられる
線形移流方程式
CFDで流れを計算するために解くナビエ・ストークス方程式は下記のとおりです。

この中で右辺を全て取り除き、非定常項と移流項だけの関係式を移流方程式と呼びます。ただ、この式だと移動する物性値vと移動する速度vが同じなので、非線形方程式になります。
流体は、速度だけではなく熱やVOF値も運びます。そのため、本講座では適用範囲を広げるために移流方程式を線形にします。移動する物性値 u 、速度 c とすると下記のような式になります。
$$ \frac{\partial v}{\partial t} + c \frac{\partial v}{\partial x} = 0$$
ここまで単純化することで、時間とともに流体が物性値を運ぶ様子だけを捉えることができます。
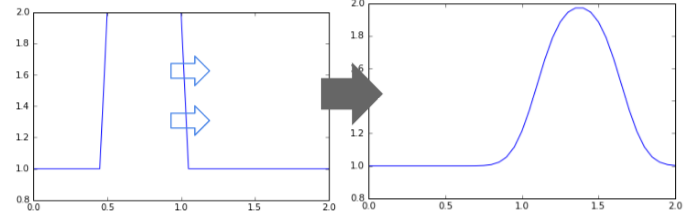
下記は物性値を運ぶ様子をプロットした図です。初期条件では物性値uはx=0.5~1.0の範囲でu=1、それ以外では0を与えています。移流方程式を解くことで、物性値が流れ方向に進むことがわかります。
風上差分
移流項の離散化手法としては風上差分が最も有名です。風上差分は下記の式で表せます。
\frac {\partial v} {\partial x} \approx c \frac{v_{i}-v_{i-1}}{\Delta x} $$
特に右辺の分子に注目してください。中心差分ではi点の両端を使用していましたが、風上差分ではi点とi-1点という隣り合った値を使用します。隣り合った値を参照することで、格子幅の大きさの波まで捉えることができるので振動が起きにくくなります。
風上差分は安定性は高い一方で、人工粘性が入っているぶん精度は下がります。
それでは、まずは風上差分のプログラムから見ていきましょう。
風上差分プログラム
下記が風上差分のプログラムになります。初めなので、丁寧に解説していきます。
Pythonで書かれていますので、Pythonの環境を整えてください。jupyter notebookがおすすめです。
Pythonは非常に見やすい言語なので、プログラミングが初めての方でも比較的とっつきやすいと思います。
import numpy
import matplotlib.pyplot as plt
%matplotlib inline
nx = 501
dx = 2 / (nx - 1)
nt = 1000
dt = .001
c = 1
u = numpy.zeros(nx)
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1
for n in range(nt):
u_old = u.copy()
u[1:-1] = u_old[1:-1] - c * dt / dx * (u_old[1:-1] - u_old[:-2])
#for i in range(1, nx-1):
# u[i] = u_old[i] - c * dt / dx * (u_old[i] - u_old[i-1])
if n % 200 == 0:
plt.plot(numpy.linspace(0, 2, nx), u)
plt.show()
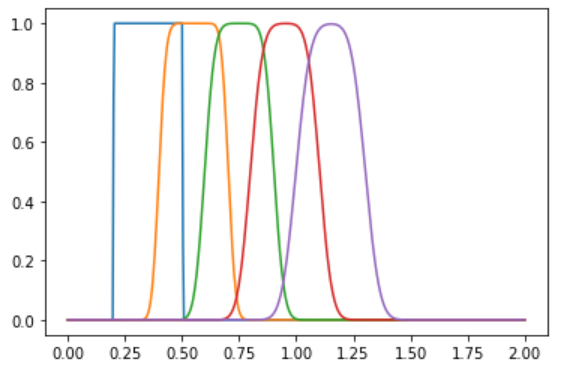
上記のプログラムを実行すると、出力結果として下記のグラフが得られます。
ライブラリ
上から順にプログラムを解説していきます。まずは使用するライブラリのインポートからです。
import numpy
import matplotlib.pyplot as plt
%matplotlib inline使うライブラリはnumpyとmatplotlibです。import 〇〇と書くことでライブラリをインポートでき、as〇〇と書くことで別名を定義できます。
numpyは配列演算に関するライブラリです。まとめてデータを扱えて計算が高速であることから、数値計算では非常によく使われます。npという省略表記されることも多いです。
pythonにはリストという機能がありますが、今回はnumpyを使用します。numpyでは格納される型が揃っており、他のライブラリとの相性の面でも使い勝手がよいです。
matplotlibはグラフ描画用ライブラリです。計算結果を可視化するために使用します。
今回はmatplotlib内のpylotというメソッドを多用するので、pltという省略名で定義しておきます。これによってplt.〇〇という表記で使用することができ、プログラムがスッキリします。
初期化
ここでは解析の初期条件を与えます。
初期条件として、格子数や時間刻み幅などのパラメータから、どこにどのくらいの速度を与えるかまで決定してやる必要があります。
nx = 501
dx = 2 / (nx - 1)
nt = 1000
dt = .001
c = 1
u = numpy.zeros(nx)
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1 nxは格子の節点数です。nxは節点なのでセル数はnx-1個になることは注意してください。今回から説明する差分法では計算点が節点になります。そのため、501点の計算点があると考えてください。
dxは接点間距離です。セルの大きさと言い換えてもらっても良いです。
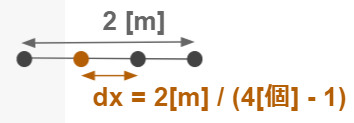
今回は計算領域の長さを2mとするため、このような式となっています。複雑そうに見える場合は下記の節点が少ない場合の例を表した図を見ると、わかりやすいと思います。
節点が両端に位置することになるので、接点間距離はnx-1個の間隔で割ることがわかります。
ntはステップ数です。今回はforループで時間を進めるので、1000回ループ計算を行うことになります。言い換えると、1000回も移流方程式を解くことになります。
dtは時間刻み幅です。1回のステップで進む時間を表します。CFDでは時間刻み幅は非常に重要な要素です。計算の安定化のために調節してやる必要があります。
cは流速(速度)です。線形移流方程式なので、流速は定数になります。
uは輸送される任意の変数です。ナビエ・ストークス方程式なら流速、熱やVOF値の場合もあります。初期値として、0.2~0.5の範囲で1を与えてやります。他は0に設定しているので、 0.2~0.5の範囲だけ1となる矩形波が現れます。
移流方程式(風上差分)
ここからがメインの計算ループになります。
今回は矩形波を時間経過とともに右側に流すプログラムになるので、時間をforループで進めます。
for n in range(nt):
u_old = u.copy()
u[1:-1] = u_old[1:-1] - c * dt / dx * (u_old[1:-1] - u_old[:-2])
#for i in range(1, nx-1):
# u[i] = u_old[i] - c * dt / dx * (u_old[i] - u_old[i-1])
・・・nステップを0~ ntまで変化させて時間変化を計算します。forループ内に移流方程式が入ります。
u_oldは古い時間ステップにおける輸送変数uの値です。uの値は移流方程式で更新されるため、u_oldを右辺において新しい値はuに代入することとします。
pythonでは配列をまとめて演算するのでこのような一時変数は不要ですが、他の言語にも対応できるように一般的な書き方をしています。
次の行は、移流方程式を風上差分で書いた式です。下記の式をプログラム化しています。
$$ u^{n+1} = c \Delta t \frac{u_{i}-u_{i-1}}{\Delta x} $$
配列の範囲が1:-1となっているのは、領域の両端の節点では移流方程式を計算していないからです。両端の節点は参照点としてだけ使用します。風上は左隣りの点なので、[0:-2](0は省略)となっています。
これは、移流方程式を風上差分で離散化した際に、計算点の隣の節点を参照するためです。そのため、端の計算点は計算出来ないことになります。
(厳密には風上側の端だけが計算できません。プログラムをわかりやすくするために両端の節点を計算から外しています)
離散化スキームの変更には、この1行を変更すれば良いことがわかります。
#(シャープ)でコメントアウトしているのは、for文で書いた場合の移流方程式です。この形であれば、他の言語にも使用できます。
式の形は変わりませんが、for文で書いた場合は要素が一つずつ変更されていくので、u_oldが重要になります。
グラフ描画
グラフ描画には、初めにインポートしたグラフ描画ライブラリのmatplotlibを使用します。
for n in range(nt):
・・・
if n % 200 == 0:
plt.plot(numpy.linspace(0, 2, nx), u)
plt.show()
for文の中にif文があります。ここで、時間ステップが200進むごとに画面出力をしています。
plt.plotはグラフの描画を行います。横軸と縦軸を指定することでグラフを描画できます。
横軸はnumpy.linspaceを使用します。linspaceは指定した範囲を等間隔で分割した配列を作成してくれます。ここでは横軸には0~2までをnx分割し、縦軸はuを使用することにより、縦横で同じ要素数の配列を作成できます。
最後のplt.showはグラフの画面表示です。plotは描画に対してshowは表示です。plotでグラフを重ねて描画し、showでまとめて表示しています。
結果として下記のようなグラフが出力されます。

初期状態では0.2~0.5までを1とする矩形波だった波が、右側に移動していっていることがわかります。
ただし、風上差分の欠点は、波が滑らかになってしまっていることです。本来は矩形波のまま移動するはずだった波が人工粘性により曲線になってしまいました。
一方で、風上差分は非常に安定した計算のできる手法であることから、よく使用されます。多くの高精度かつ安定的な手法がありますが、基本は風上差分とこれから紹介する中心差分がもととなっています。特に、風上に参照点を取ると安定化するという考え方は非常に重要ですので、頭の片隅に残しておいてください。
中心差分
風上差分は波が滑らかになってしまいましたが、これは粘性誤差による影響です。i点の計算のために、i点とi-1点を参照するというのは違和感があったと思います。
これはもともとは中心差分ありきの考え方です。i点の値を計算したい場合は、普通に考えて周りの点を参照するべきです。具体的には、i点を計算するために、隣のi-1点とi+1点を使うべきでしょう。それが中心差分です。
中心差分は下記のような式で表されます。
$$ c \frac{\partial v}{\partial x} \approx c \frac{v_{i+1}-v_{i-1}}{2\Delta x} $$
離散化すると誤差が発生するので、完全にイコールの式にはなっていません。中心差分では、分子は速度vに関して節点iの両端のi+1とi-1、分子は格子幅の2倍となっています。
両端の節点を使っているというのがポイントで、このような参照の仕方をすることで理論的な誤差を抑えられます。ただし一方で、計算が不安定になり、急激に数値振動が増大するようになります。実際に計算した結果は下記のようになります。右に流れる矩形波を一定時間毎にプロットしていますが、動いてすぐに振動が増大していることが分かります。
実用的ではないですが、今後の理解のためにも、基本として中心差分の書き方を知っておきましょう。
中心差分プログラム
中心差分に書き換えたものが下記になります。移流方程式の参照点と時間刻み幅dtのみ変更しています。
中心差分は不安定になりやすいので、dtをかなり小さくとっています。
#中心差分
import numpy
import matplotlib.pyplot as plt
%matplotlib inline
nx = 501
dx = 2 / (nx - 1)
nt = 1000
dt = .0002 #変更
c = 1
u = numpy.zeros(nx)
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1
for n in range(nt):
u_old = u.copy()
u[1:-1] = u_old[1:-1] - c * dt / (2 * dx) * (u_old[2:] - u_old[:-2])
#for i in range(1, nx-1):
# u[i] = u_old[i] - c * dt / (2 * dx) * (u_old[i+1] - u_old[i-1])
if n % 200 == 0:
plt.plot(numpy.linspace(0, 2, nx), u)
plt.show()
移流方程式(中心差分)
変化部分は移流項の参照点だけなので、そこだけ説明します。
今回も矩形波を時間経過とともに右側に流すプログラムになるので、時間をforループで進めます。
for n in range(nt):
u_old = u.copy()
u[1:-1] = u_old[1:-1] - c * dt / (2 * dx) * (u_old[2:] - u_old[:-2])
#for i in range(1, nx-1):
# u[i] = u_old[i] - c * dt / (2 * dx) * (u_old[i+1] - u_old[i-1])
・・・nステップを0~ ntまで変化させて時間変化を計算します。forループ内に移流方程式が入ります。
u_oldは古い時間ステップにおける輸送変数uの値です。uの値は移流方程式で更新されるため、u_oldを右辺において新しい値はuに代入することとします。
次の行は、移流方程式を中心差分で書いた式です。下記の式をプログラム化しています。
$$ u^{n+1} = c \Delta t \frac{u_{i+1}-u_{i-1}}{\Delta x} $$
uの配列の範囲が[1:-1]となっているのは、領域の両端の節点では移流方程式を計算していないからです。両端の節点は参照点としてだけ使用します。中心差分の参照点は、[1:-1]の左右に当たるので、[2:]、[:-2]となります。
風上差分から中心差分への変更には、この1行を変更すれば良いです。
#(シャープ)でコメントアウトしているのは、for文で書いた場合の移流方程式です。この形であれば、他の言語にも使用できます。
式の形は変わりませんが、for文で書いた場合は要素が一つずつ変更されていくので、u_oldが重要になります。
出力結果は下記のようになります。
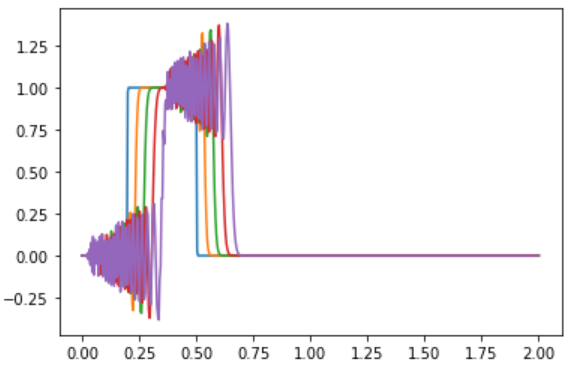
時間刻み幅dtを小さくしたのに、大きな振動が起きてしまっています。こうなってしまうと実用性は皆無です。そのため、風上差分などの適度に振動を抑えるような粘性を加えた手法が使われているのが現象です。
おわりに
今回は風上差分と中心差分について解説しました。Pythonのプログラムはこれからの解説でも使用しますので、保存しておいてください。
今回はPythonでプログラミングを行ったので、Pythonのみやすさを理解していただけたと思います。最終的には高速化のためにC++などを使用することになるかもしれませんが、Pythonは他にも色々役に立つのでぜひ身に付けておくことをオススメします。
今回重要な項目は下記のとおりです。
- 風上差分は数値的に安定するが、誤差が大きい
- 風上差分は誤差により波がなめらかになる
- 中心差分は誤差は少ないが、数値振動が起きる
- 中心差分は計算が不安定なので、実用性はない
- CFDプログラミングは、「変数定義→初期化→実行→可視化」の流れである
- CFDプログラミングには、numpyとmatplotlibを使う
- numpyは配列ライブラリでmatplotlibはグラフ描画ライブラリである
今回の内容は、これからのCFDプログラム講座の基本となります。重要な部分は繰り返し説明しますが、わからないところはじっくり見て理解してからすすめるようにしてください。
次回はLax-Wendroff法について解説します。
Lax-Wendroff法は多項式にすることで精度を上げた手法です。風上差分と中心差分の中間的な存在になります。これから紹介する手法は、安定性と精度の両立を目指したものです。そのための工夫を見ていくと全体像がつかめてわかりやすいと思います。
Youtubeもやってます
youtubeでも解説しています。2回分の内容が含まれているので少しボリュームがありますね。
 ITとCFD入門サイト
ITとCFD入門サイト 

