格子法入門第11回は、偏微分方程式の分類分けである「双曲型・放物型・楕円型」について説明します。
前回は空間スキームであるハイブリッド法・べき乗法・TVDスキームについて説明しました。下記からどうぞ。
重要なポイントは下記の通りです。
- ペクレ数は移流と粘性の比の指標である
- ハイブリッド法は、ペクレ数Pe=2を境に風上差分と中心差分を切り替える
- べき乗法は、ペクレ数が大きいときは粘性をゼロとし、ペクレ数が小さいときはべき乗則を使う
- TVDスキームは、流速制限関数によりスキームが切り替わる
特にTVDスキームは流体解析を安定させるためによく利用される空間スキームです。理解しておくと非常に役に立つでしょう。
双曲型・放物型・楕円形
さて今回は基本に戻って、偏微分方程式に関するお話です。
流体解析で使用するナビエ・ストークス方程式は、ご存知の通り偏微分方程式です。

そして、ナビエ・ストークス方程式は一般解がなく、項を分解して簡単な式に変換してから解きます。
その際に出てくるのが、「双曲型・放物型・楕円形」といった表現です。
2階偏微分方程式
双曲型・放物型・楕円形というのは、2階微分方程式を特徴に応じて3つに分類したものです。
2階微分方程式は一般的に以下のように書けます。
$$ A \frac{\partial^2 \phi}{\partial x^2} + 2B \frac{\partial^2 \phi}{\partial x \partial y} + C \frac{\partial^2 \phi}{\partial y^2} = D$$
ここで$\lambda$を定義します。
$$ \lambda = B^2 – AC $$
この$\lambda$の符号によって、2階微分方程式が3つの特徴に分類できます。
$\lambda > 0$ なら双曲型であり、流体解析では移流方程式に当たります。
移流方程式は、ナビエ・ストークス方程式の非定常項と移流項だけで構成された式です。
$\lambda = 0$ なら放物型であり、流体解析では拡散方程式に当たります。
拡散方程式は、ナビエ・ストークス方程式の非定常項と拡散項だけで構成された式です。
$\lambda > 0$ なら楕円型であり、流体解析ではラプラス(もしくはポアソン)方程式に当たります。
ラプラス(ポアソン)方程式は、ナビエ・ストークス方程式の圧力項を計算する際に使用します。
つまり、ナビエ・ストークス方程式は3つの特徴が全て入った式であると言えます。
ここからは、それぞれの特性について見ていきましょう。
双曲型($\lambda > 0$)
波動方程式が双曲型に当たります。波動方程式は下記で表されます。
$$ \frac{\partial^2 \phi}{\partial t^2} – c^2 \frac{\partial^2 \phi}{\partial x^2} = 0$$
ここで、$t$は時間、$x$は空間座標です。この式は2つの1階微分方程式に分けることができます。
$$ \frac{\partial \phi}{\partial t} = – c \frac{\partial \phi}{\partial x}$$
$$ \frac{\partial \phi}{\partial t} = + c \frac{\partial \phi}{\partial x}$$
この2つは移流方程式と呼ばれ、速度$c$で伝わる流れを表しています。
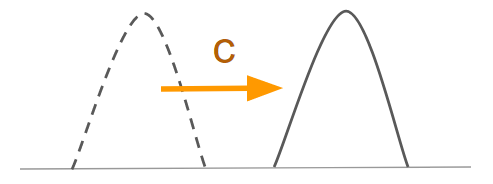
2つの式は符号が異なるため、流れの向きが逆向きであることを意味します。
格子法による流体解析では、移流方程式の右辺の空間一次微分項がやっかいで、誤差の原因となります。
放物型($\lambda = 0$)
非定常拡散方程式が放物型にあたります。非定常拡散方程式は下記で表されます。
$$ \frac{\partial \phi}{\partial t} = \alpha \frac{\partial^2 \phi}{\partial x^2}$$
$\alpha$ は拡散係数で、時間とともに値が広がることを表しています。
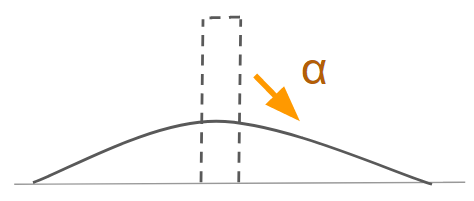
双曲型との大きな違いは、影響範囲です。
双曲型では、速度$c$の範囲でしか影響がありませんでしたが、放物型ではすべての範囲に影響します。
例えば、1ヶ所だけ極大値を取り他は0の計算領域であっても、時間が経つと全て非ゼロの値となります。
これは、無限の伝搬速度を意味しており非現実的です。
実際の計算では、離散化により影響範囲が制限されるため、このような問題は起こりません。
楕円型($\lambda < 0$)
ラプラス方程式やポアソン方程式が楕円形にあたり、どちらも定常拡散方程式を意味します。
$$ \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} = 0 $$
$$ \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} = S (x,y) $$
ラプラス方程式は右辺がゼロ、ポアソン方程式は右辺にソース項があります。
流体解析でナビエ・ストークス方程式を扱う場合、通常はポアソン方程式により圧力計算が行われます。
名前に「定常」とついている通り、時間変化はありません。双曲型や放物型のような初期値は不要で、境界条件さえあれば解くことができます。
ポアソン方程式で重要なのは、ソース項の存在です。
計算領域の一部でソース項を変更するだけで、領域全ての値が変化します。これは、ピンと張った布の一部を引っ張り上げたときに全ての布の位置がずれるのと同じです。
流体解析では圧力計算でポアソン方程式が使用されますが、変化が領域全てに影響するというのは意外と厄介です。
放物型と同様に、普通に離散化を行うと影響範囲が制限されてしまいますが、圧力は流れへの影響が大きいため、このようなごまかしが効きません。正確な計算が求められます。
そこでポアソン方程式に対しては、十分に圧力の勾配が収まるまで収束計算するのが一般的です。
収束計算が含まれるため、圧力計算は流体解析では負荷の高い計算となります。
おわりに
今日は、双曲型・放物型・楕円型の3つについて説明しました。
重要なポイントは下記の通りです。
- 2階微分方程式は、双曲型・放物型・楕円型の3つに分けられる
- 移流方程式は双曲型にあたる
- 非定常拡散方程式は放物型にあたる
- 定常拡散方程式は楕円型にあたる
- 楕円型であるポアソン方程式には、収束計算が使われる
双曲型・放物型・楕円型という呼び方は数学的な表現です。
流体解析を学ぶなら、頭の中で「移流」「拡散」「圧力」くらいに置き換えてもらっても問題もありません。つまり、これらは慣れ親しんだ計算であり、特別難しいことではないということです。
ぜひこの機会に数学的表現の苦手意識を克服してみてください。
 ITとCFD入門サイト
ITとCFD入門サイト 

