今回は、ハイブリッド法(hybrid differencing scheme)とべき乗法(power-low scheme)とTVDスキームについて説明します。
前回はレベルセット法について説明しました。下記からどうぞ。
レベルセット法に関して、重要なポイントは下記のとおりです。
- 界面を捉える手法である
- 境界を$\phi = 0$とする関数を使用する
- 界面の分割にも対応できる
- レベルセット関数の傾きにより、法線ベクトルの取得が容易である
- レベルセット関数の定義の崩れを防ぐために最初期化を行う
さて今回は大きく話が変わって、ハイブリッド法(hybrid differencing scheme)とべき乗法(power-low scheme)とTVDスキームについて説明します。
はじめ2つはペクレ数に応じてスキームを変更する手法であり、安定性と精度に優れる手法です。
一方で、TVDスキームは流速制限を使うことで、安定性と精度を両立した手法です。
ペクレ数
ペクレ数は、対流と対流の相対的な強さを表す指標であり、下記の式で得られます。
$$ Pe = \frac{F}{D} = \frac{\rho u}{\Gamma / \delta x} $$
Fは対流、Dは粘性を表します。$\rho$は密度、uは流速、$\Gamma$は粘性係数、$\delta x$は代表長さを表します。
拡散だけの場合は、$Pe = 0$となり、周囲の計算点の影響を受けます。
移流だけの場合は、$Pe = \infty$となり、片方(上流側)の影響を受けます。
ハイブリッド法 (hybrid differencing scheme)
ハイブリッド法は、ペクレ数に応じて風上差分と中心差分を切り替える手法です。
ペクレ数$Pe=2$を境目として、下記のような条件で切り替えます。
$$ Pe \geq 2 : 風上差分$$
$$ Pe < 2 : 中心差分$$
ペクレ数が大きいということは移流項が支配的であるため、計算が不安定になりやすいです。そのため、風上差分にて数値粘性を与えて安定化させます。
風上差分を使用するため、最低精度が一次精度となります。
一方で、ペクレ数が小さいときは粘性が高いため、計算が比較的安定します。そのため、精度の高い中心差分を使用します。
中心精度を使用するため、最高精度は二次精度となります。
よって、ハイブリッド方では流体のペクレ数に応じて精度が変わることがわかります。
ハイブリッド法では、常に輸送性を満たす(妥当な解が得られる)ことがわかっています。つまり、必ず安定するということです。
ただ、最低精度が一次精度であるため、偽拡散による誤差が発生しやすいという問題があります。
べき乗法 (power-low scheme)
べき乗法は厳密解を正確に近似するため、ハイブリッド法よりも良い結果が得られます。
べき乗法では、ペクレ数$Pe>10$で拡散を0とします。
$$ q_{i-1} = F_{i-1} \fai_{i-1} $$
ペクレ数 $0<Pe<10$ で流速を多項式で近似します。
$$ q_{i-1} = F_{i-1} [\fai_{i-1} – \beta_{i-1} (\fai_i \fai_{i-1})] $$
$$ \beta_{i-1} = \frac{( 1 – 0.1 Pe_{i-1} )^5}{ Pe_{i-1} }$$
ただし、一次精度であるという難点もあります。
TVDスキーム
TVDスキームとは一言でいうと、単調性を維持するためにスキームを変える手法です。単調性とは、時間とともに変動が大きくならないという条件です。
TV(Total Variation:全変動)は、下記の式で表されます。全変動という名前の通り、隣のセルとの値の差の合計を表します。
$$ TV(u^n) = \Sigma | u^n_{j+1} – u^n_j|$$
TVD (Total Variation Diminishing:全変動減少) 条件は、時間が進んでも全変動が増加しない条件です。つまり、TVの値が時間ステップn+1になっても増加しないことになります。
条件式で書くと下記のようになります。
$$ TV(u^{n+1}) \leq TV(u^n) $$
この条件を守るように計算を行うのが、TVDスキームです。
この条件を守ることで、安定して精度の高いスキームを維持できます。
TVD条件
TVD条件を維持するためには、下記の条件を守る必要があります。
- 0 < r < 1 において g(r) = 2r & g(r) <= 2r
- 1 < r において g(r) = 2 & g(r) <= 2
rは隣接セルの勾配比を表します。勾配比なので、r=1で平坦となります。
g(r)は流束制限関数です。流束とは、セル間における流速cと輸送値uをかけたものです。
流束は移流計算でよく使用される値です。移流として計算を行うことで、移流計算式が簡単になるという特徴があります。流束はセル間の値を取るので、1/2点の値を使用していることを覚えておきましょう。
ではここからは、TVD条件を満たすための式を考えていきましょう。
下記に隣接セルの勾配値rと流束制限関数g(r)のグラフを示します。
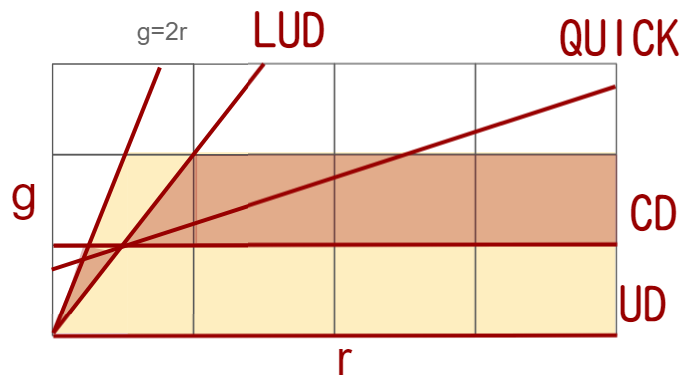
上記で示したTVD条件は、黄色と赤で色付けした部分になります。この部分が単調性を維持する領域なので、ここに収まる値であれば安定性を維持できます。
さらに狭い範囲である赤の部分は、二次精度を維持できます。せっかくなら精度が高いほうが良いので、この赤い部分を維持するような式がたくさん提案されています。
おわりに
今回は、離散化スキームとしてハイブリッド法・べき乗法・TVDスキームについて紹介しました。
重要なポイントは下記の通りです。
- ペクレ数は移流と粘性の比の指標である
- ハイブリッド法は、ペクレ数Pe=2を境に風上差分と中心差分を切り替える
- べき乗法は、ペクレ数が大きいときは粘性をゼロとし、ペクレ数が小さいときはべき乗則を使う
- TVDスキームは、流速制限関数によりスキームが切り替わる
全てを理解する必要はなく、違いの特徴だけ頭の片隅に残しておくと良いでしょう。
これらはあくまで基本的な手法であり、実用ではさらに高精度なWENOスキームなどが使用されます。機会があればWENOについても書きたいと思います。
 ITとCFD入門サイト
ITとCFD入門サイト 

