この講座ではPythonを使用したCFDプログラミングを解説していきます。最後まで受講して頂くと、差分法による流体解析ができるようになるようにしています。ぜひ最後までお付き合いください。
第2回からは移流項に関する解説をしていきます。移流項は最も難しい部分ですが、特に重要なので先に解説します。
前回の第6回では移流方程式の離散化スキームであるCIP法について解説しました。まだ見てない方は下記からどうぞ。
重要な項目は下記の通りです。 CIP法は傾きを使用するという特殊な手法です。しかし、そのおかげで参照点が少なくても十分な精度を得ることができます。実際、今まで紹介した離散化スキームの中で最も波形状を維持できます。
- CIP法は、少ない参照点から多くの情報が得られる
- CIP法は傾きの情報があるため、急激な値変化に対する安定性が高い
- CIP法では1ステップの移動距離$\xi$を使用する
- CIP法では、全てのセルにおける物性値の微分値$g_i$を計算する
ただし、CIP法は微分値を使うため、二次元にしたときに複雑な式になります。これはフラクショナルステップ法などによって簡易化が行われます。しかし、フラクショナルステップ法は精度低下の原因にもなるので、このあたりは労力と精度の優先度の比較が必要です。
そこで、今回は二次元への拡張も簡単なTVDスキームというものを紹介します。
TVDスキーム
TVDスキームとは一言でいうと、単調性を維持するためにスキームを変える手法です。単調性とは、時間とともに変動が大きくならないという条件です。
TV(Total Variation:全変動)は、下記の式で表されます。全変動という名前の通り、隣のセルとの値の差の合計を表します。
$$ TV(u^n) = \Sigma | u^n_{j+1} – u^n_j|$$
TVD (Total Variation Diminishing:全変動減少) 条件は、時間が進んでも全変動が増加しない条件です。つまり、TVの値が時間ステップn+1になっても増加しないことになります。
条件式で書くと下記のようになります。
$$ TV(u^{n+1}) \leq TV(u^n) $$
この条件を守るように計算を行うのが、TVDスキームです。
この条件を守ることで、安定して精度の高いスキームを維持できます。
TVD条件
TVD条件を維持するためには、下記の条件を守る必要があります。
- 0 < r < 1 において g(r) = 2r & g(r) <= 2r
- 1 < r において g(r) = 2 & g(r) <= 2
rは隣接セルの勾配比を表します。勾配比なので、r=1で平坦となります。
g(r)は流束制限関数です。流束とは、セル間における流速cと輸送値uをかけたものです。
流束は移流計算でよく使用される値です。移流として計算を行うことで、移流計算式が簡単になるという特徴があります。流束はセル間の値を取るので、1/2点の値を使用していることを覚えておきましょう。
ではここからは、TVD条件を満たすための式を考えていきましょう。
下記に隣接セルの勾配値rと流束制限関数g(r)のグラフを示します。
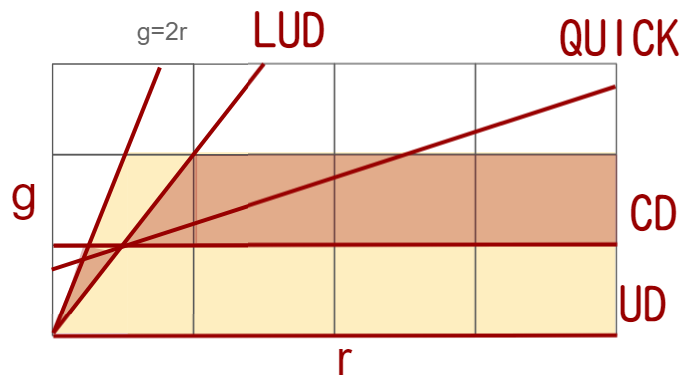
上記で示したTVD条件は、黄色と赤で色付けした部分になります。この部分が単調性を維持する領域なので、ここに収まる値であれば安定性を維持できます。
さらに狭い範囲である赤の部分は、二次精度を維持できます。せっかくなら精度が高いほうが良いので、この赤い部分を維持するような式がたくさん提案されています。
minmod
$$ g(r) = \max(0,\min(r,1)) $$
van Leer
$$ g(r) = \frac{r + |r|}{1+r} $$
MUSCL
$$ g(r) = \max(0,\min(2r,(1+r)/2,2)) $$
Harten-Yeeのnon-MUSCL型TVDスキーム
$$ g(r) = sign(\alpha_{i+ \frac{1}{2}})\max(\min(|\alpha_{i+ \frac{1}{2}}|, sign(\alpha_{i+ \frac{1}{2}})\alpha_{i-\frac{1}{2}}),0)) $$
今回は最後の Harten-Yeeのnon-MUSCL型TVDスキーム を使用します。
今回使用する式
まず、今回は流束がキーとなるので、事前にセル間の値である1/2点の値を計算します。ここでは、$u_{i+1/2}$の値を$\alpha_{i+1/2}$とします。
$$ \alpha_{i + \frac{1}{2}} = u^{old}{i+1} – u^{old}{i} $$
意味のないように見えるかもしれませんが、プログラム上の配列では1/2点を表すことができないため、alpha[i]に$\alpha_{i+1/2}$の値が入ることになります。
このようにセル間である1/2点の管理のために、$alpha$を導入しています。
次は流束制限関数g(r)です。
$$ g_i = minmod(\alpha_{i-\frac{1}{2}},\alpha_{i+ \frac{1}{2}}) $$
g(r)は流束制限関数の名の通り、セル間の値を使用して計算していることに注意してください。
minmod関数は下記のような中身になります。
$$ minmod(\alpha_{i-\frac{1}{2}},\alpha_{i+ \frac{1}{2}}) = sign(\alpha_{i+ \frac{1}{2}})\max(\min(|\alpha_{i+ \frac{1}{2}}|, sign(\alpha_{i+ \frac{1}{2}})\alpha_{i-\frac{1}{2}}),0)) $$
minmod関数はTVD条件の 隣接セルの勾配値rと流束制限関数g(r)の関係を表したグラフにプロットすると、下記のような線が引かれます。
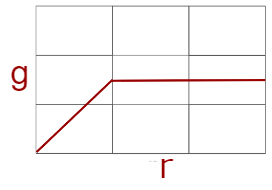
minmod関数を使うことで二次精度を得られます。
流束制限関数が得られたので、最後の物性値の更新までの計算を行います。
流束制限関数から物性値uの更新までの計算式が長いので、一時変数をいくつか用意します。 $\beta$にはゼロ割を防ぐ項が含まれます。
$$ \sigma = \frac{1}{2} (|c| – \frac{\Delta t}{\Delta x}c^2) $$
$$ \beta_{i+ \frac{1}{2}} = \frac{\sigma (g_{i+1} – g_{i}) \alpha_{i+ \frac{1}{2}}}{\alpha_{i+ \frac{1}{2}}^2 + 10^{-20}} $$
$$ \Phi = \sigma(g_i + g_{i+1})-|c + \beta_{i+ \frac{1}{2}}| \alpha_{i+ \frac{1}{2}}) $$
上記3つは一次変数です。下記の流束Fの計算に使用します。
$$ F_{i+ \frac{1}{2}} = \frac{1}{2} (c u^{old}_{i+1} + c u^{old}_i + \Phi) $$
流束Fの計算において、普通に流束を計算すると流速cと輸送値uの掛け算なので、$ c u^{old}_{i+1} + c u^{old}_i $ で表せます。それに対し、上記の式では$ \Phi $ が追加で足されていることがわかります。
最後に流束から次の時間ステップの輸送値$u^{n+1}$を計算します。
$$ u_i = u^{old}i – \frac{\Delta t}{\Delta x}(F{i+ \frac{1}{2}} – F_{i- \frac{1}{2}})$$
以上が Harten-Yeeのnon-MUSCL型TVDスキームになります。
TVDスキーム
TVDスキームを使用したコードは下記の通りです。今回は Harten-Yeeのnon-MUSCL型TVDスキーム を使用します。
今までに比べると少し長いプログラムになります。
import numpy as np
import matplotlib.pyplot as plt
nx = 501
dx = 2 / (nx - 1)
nt = 1000
dt = .001
c = 1
u = np.zeros(nx)
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1
alpha = np.zeros(nx)
g = np.zeros(nx)
flux = np.zeros(nx)
for t in range(nt):
u_old = u.copy()
alpha[:-1] = u_old[1:] - u_old[:-1]
for i in range(1,nx-1):
g[i] = (np.sign(alpha[i]) *
max(min(abs(alpha[i]), np.sign(alpha[i])
* alpha[i-1]),0.0))
sigma = 0.5 * (np.abs(c) - dt/dx * c ** 2)
beta = (sigma * (g[1:] - g[:-1])
* alpha[:-1] / (alpha[:-1]**2 + 1e-20))
phi = (sigma * (g[:-1] + g[1:])
- abs(c + beta) * alpha[:-1])
flux[:-1] = 0.5 * (c * u_old[1:] + c * u_old[:-1] + phi)
u[1:-1] = (u_old[1:-1] - dt / dx *
(flux[1:-1] - flux[:-2]))
if t % 200 == 0:
plt.plot(np.linspace(0,2,nx),u)
plt.show()
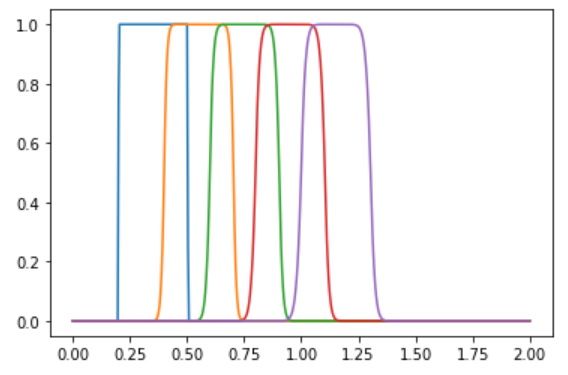
出力結果は下記のようになります。 全く計算不安定が現れておらず、非常に安定した結果です。しかも、波の形状も維持できており、非常に良い結果が得られていることがわかります。
ライブラリ
上から順にプログラムを解説していきます。まずは使用するライブラリのインポートからです。
import numpy
import matplotlib.pyplot as plt
%matplotlib inline使うライブラリはnumpyとmatplotlibです。import 〇〇と書くことでライブラリをインポートでき、as〇〇と書くことで別名を定義できます。
numpyは配列演算に関するライブラリです。まとめてデータを扱えて計算が高速であることから、数値計算では非常によく使われます。npという省略表記されることも多いです。
pythonにはリストという機能がありますが、今回はnumpyを使用します。numpyでは格納される型が揃っており、他のライブラリとの相性の面でも使い勝手がよいです。
matplotlibはグラフ描画用ライブラリです。計算結果を可視化するために使用します。
今回はmatplotlib内のpylotというメソッドを多用するので、pltという省略名で定義しておきます。これによってplt.〇〇という表記で使用することができ、プログラムがスッキリします。
初期化
ここでは解析の初期条件を与えます。
初期条件として、格子数や時間刻み幅などのパラメータから、どこにどのくらいの速度を与えるかまで決定してやる必要があります。
nx = 501
dx = 2 / (nx - 1)
nt = 1000
dt = .001
c = 1
u = np.zeros(nx)
u[int(0.2 / dx) : int(0.5 / dx + 1)] = 1
alpha = np.zeros(nx)
g = np.zeros(nx)
flux = np.zeros(nx)nxは格子の節点数です。nxは節点なのでセル数はnx-1個になることは注意してください。今回から説明する差分法では計算点が節点になります。そのため、501点の計算点があると考えてください。
dxは接点間距離です。セルの大きさと言い換えてもらっても良いです。
今回は計算領域の長さを2mとするため、このような式となっています。複雑そうに見える場合は下記の節点が少ない場合の例を表した図を見ると、わかりやすいと思います。
節点が両端に位置することになるので、接点間距離はnx-1個の間隔で割ることがわかります。
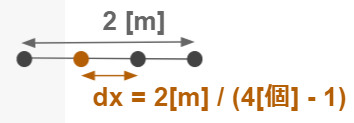
ntはステップ数です。今回はforループで時間を進めるので、1000回ループ計算を行うことになります。言い換えると、1000回も移流方程式を解くことになります。
dtは時間刻み幅です。1回のステップで進む時間を表します。CFDでは時間刻み幅は非常に重要な要素です。計算の安定化のために調節してやる必要があります。
cは流速(速度)です。線形移流方程式なので、流速は定数になります。
uは輸送される任意の変数です。ナビエ・ストークス方程式なら流速、熱やVOF値の場合もあります。初期値として、0.2~0.5の範囲で1を与えてやります。他は0に設定しているので、 0.2~0.5の範囲だけ1となる矩形波が現れます。
alphaは隣接セル値の差です。具体的には、$u_{i+1}$と$u_i$の差です。ここでは初期化だけ行います。
gは流速制限関数です。隣接したalphaの値の差が大きくなりすぎると計算が不安定になるため、調整をします。ここでは初期化のみ行います。
fluxは流束です。流束は流速cとセル値uをかけたもので、セル間の値である1/2点の値を取ります。今まではuをそのまま使用していましたが、流束fluxで表すのが一般的です。
移流方程式(TVDスキーム)
ここからがメインの計算ループになります。
今回は矩形波を時間経過とともに右側に流すプログラムになるので、時間をforループで進めます。
for t in range(nt):
u_old = u.copy()
alpha[:-1] = u_old[1:] - u_old[:-1]
for i in range(1,nx-1):
g[i] = (np.sign(alpha[i]) *
max(min(abs(alpha[i]), np.sign(alpha[i])
* alpha[i-1]),0.0))
sigma = 0.5 * (np.abs(c) - dt/dx * c ** 2)
beta = (sigma * (g[1:] - g[:-1])
* alpha[:-1] / (alpha[:-1]**2 + 1e-20))
phi = (sigma * (g[:-1] + g[1:])
- abs(c + beta) * alpha[:-1])
flux[:-1] = 0.5 * (c * u_old[1:] + c * u_old[:-1] + phi)
u[1:-1] = (u_old[1:-1] - dt / dx *
(flux[1:-1] - flux[:-2]))
・・・nステップを0~ ntまで変化させて時間変化を計算します。forループ内に移流方程式が入ります。
u_oldは古い時間ステップにおける輸送変数uの値です。uの値は移流方程式で更新されるため、u_oldを右辺において新しい値はuに代入することとします。CIP法では、uの微分値gも同じように扱います。
pythonでは配列をまとめて演算するのでこのような一時変数は不要ですが、他の言語にも対応できるように一般的な書き方をしています。
次の行からは、移流方程式をTVDスキームで書いた式です。まずは、a,bの計算のために、下記の式をプログラム化しています。
事前にセル間の値である1/2点の値を計算します。$u_{i+1/2}$の値を$\alpha_{i+1/2}$とします。
$$ \alpha_{i + \frac{1}{2}} = u^{old}{i+1} – u^{old}{i} $$
alpha[i] に $\alpha_{i+1/2}$の値が入っていることに注意してください。
次は流束制限関数g(r)です。
$$ g_i = minmod(\alpha_{i-\frac{1}{2}},\alpha_{i+ \frac{1}{2}}) $$
$$ minmod(\alpha_{i-\frac{1}{2}},\alpha_{i+ \frac{1}{2}}) = sign(\alpha_{i+ \frac{1}{2}})\max(\min(|\alpha_{i+ \frac{1}{2}}|, sign(\alpha_{i+ \frac{1}{2}})\alpha_{i-\frac{1}{2}}),0)) $$
g(r)は流束制限関数の名の通り、セル間の値alphaを使用して計算していることに注意してください。
あとは一時変数の計算です。全てセル間である1/2点の値です。$\beta$にはゼロ割を防ぐ項が含まれます。
$$ \sigma = \frac{1}{2} (|c| – \frac{\Delta t}{\Delta x}c^2) $$
$$ \beta_{i+ \frac{1}{2}} = \frac{\sigma (g_{i+1} – g_{i}) \alpha_{i+ \frac{1}{2}}}{\alpha_{i+ \frac{1}{2}}^2 + 10^{-20}} $$
$$ \Phi = \sigma(g_i + g_{i+1})-|c + \beta_{i+ \frac{1}{2}}| \alpha_{i+ \frac{1}{2}}) $$
流束も計算します。これもセル間である1/2点の値です。
$$ F_{i+ \frac{1}{2}} = \frac{1}{2} (c u^{old}_{i+1} + c u^{old}_i + \Phi) $$
最後に流束を参考に輸送値uを更新すれば完了です。
$$ u_i = u^{old}i – \frac{\Delta t}{\Delta x}(F{i+ \frac{1}{2}} – F_{i- \frac{1}{2}})$$
基本的に左右のセルを参照するので、配列の範囲が1:-1となっています。
ただ、1/2を使用する場面が多いので、一見すると参照の範囲が変わっているように思うかも知れません。現在の式が、節点か1/2点かどちらを参照しているかを意識してプログラムを見てください。alphaからは全て1/2点を参照しています。
グラフ描画
グラフ描画には、初めにインポートしたグラフ描画ライブラリのmatplotlibを使用します。
for n in range(nt):
・・・
if n % 200 == 0:
plt.plot(numpy.linspace(0, 2, nx), u)
plt.show()
for文の中にif文があります。ここで、時間ステップが200進むごとに画面出力をしています。
plt.plotはグラフの描画を行います。横軸と縦軸を指定することでグラフを描画できます。
横軸はnumpy.linspaceを使用します。linspaceは指定した範囲を等間隔で分割した配列を作成してくれます。ここでは横軸には0~2までをnx分割し、縦軸はuを使用することにより、縦横で同じ要素数の配列を作成できます。
最後のplt.showはグラフの画面表示です。plotは描画に対してshowは表示です。plotでグラフを重ねて描画し、showでまとめて表示しています。
結果として下記のようなグラフが出力されます。

振動もなく、矩形波野形状もかなり維持できています。TVDスキームは非常に優れた離散化スキームであることがわかります。
欠点を上げるとすれば、少しだけ波がなめらかになってしまっていることでしょうか。CIP法の結果と比べると、少し角が丸まっています。
これは、精度の問題です。2次精度で計算している事による問題なので、もっと高次の手法を使えばさらに良くなります。例えば、ENOやWENOなどがあります。
おわりに
今回は TVDスキームについて解説しました。
TVDスキームは、多項式をうまく使い分けて、安定性と精度を維持する手法でした。重要なポイントは下記のとおりです。
- TVDスキームとは、単調性を維持するためにスキームを変える手法である
- 単調性とは、時間とともに変動が大きくならないという条件である
- 変動は、隣のセルとの値の差の合計のことである
- TVDスキームでは、流束制限関数により安定性を維持する
- minmodなどの関数を使用することで、2次精度を維持したTVDスキームができる
- TVDスキームを使用することで、非常に良い結果が得られる
TVDスキームは式の理解が難しいです。しかし、基本的にはこのまま式を使用すれば良いので、流束制限関数の意味合いだけ理解しておけば問題ありません。
TVDスキームを使用することで、安定性と精度において非常に良い結果が得られることがわかりました。
これは、流束制限関数を調整することで、今までの中心差分や風上差分、QUICKなどの要素をいいとこ取りでブレンドすることができているからです。
下記グラフのUDが一次風上差分法、LUDが線形風上差分(二次風上差分)法、CDが中心差分法、QUICKはQUICK法になります。
赤の領域を取るようにすると、二次風上差分やQUICK、中心差分とカブる部分が出てくることがわかると思います。

つまり、TVDスキームはいわば総まとめのようなものです。
今回は二次精度であるTVDスキームを使用しましたが、流束制限関数を使用したさらなる高精度スキームも存在します。高精度手法であるENOやWENOに関してはまた機会があれば紹介したいと思います。
次回
ここまでが一次元の移流方程式に関する内容でした。次回からは、二次元に拡張したプログラムについて解説していきます。
二次元になっても基本は変わりません。少しプログラムを変更するだけなので、チャレンジしていきましょう。
youtubeもやってます
youtubeで解説もやってます。どうぞ。
 ITとCFD入門サイト
ITとCFD入門サイト