【CFD/格子法】乱流 ④レイノルズ応力【格子法入門 #16】

ここでは数回に分けて乱流について解説しています。

前回までは乱流モデルについて説明しました。

【CFD/格子法】　乱流　③LES【格子法入門 #15】

ここでは、乱流の基本振り返りとレイノルズ応力の補足説明をしたいと思います。

乱流発生

流れはレイノルズ数が大きくなると、層流から乱流になります。

乱流では、流れに擾乱が現れて損失が発生します。

例えば管路流れにおいて、層流では摩擦損失が流速に比例するのに対して、乱流では流速の1.75乗（平滑面）または2.0乗（粗い面）に比例します。

層流から乱流へ変わることを乱流遷移といい、そのレイノルズ数を臨界レイノルズ数といいます。

管路では臨界レイノルズ数は大体下記となることが経験的にわかっています。

$$ Re_{critical} = 2100 $$

乱流の特徴

乱流には下記の特徴があります。

時間・空間的に不規則
散逸的（エネルギーが熱に変換される）
非粘性だと発生しないが、高粘性でも発生しない

最後の項目は変と思うかもしれませんが、実は非粘性でも高粘性でも乱流は発生しません。

乱流は壁の剥離や壁付近の擾乱によって起こるため、粘性流れでしか乱流は起こりません。一方で高粘性ではレイノルズ数が低くなるので、層流となります。

乱流成分

乱流流れにおいて、流速と圧力は平均成分と乱れ成分で構成されます。

平均成分は十分な長さの時間で平均した値であり、乱れ成分は平均成分からの差分を意味します。

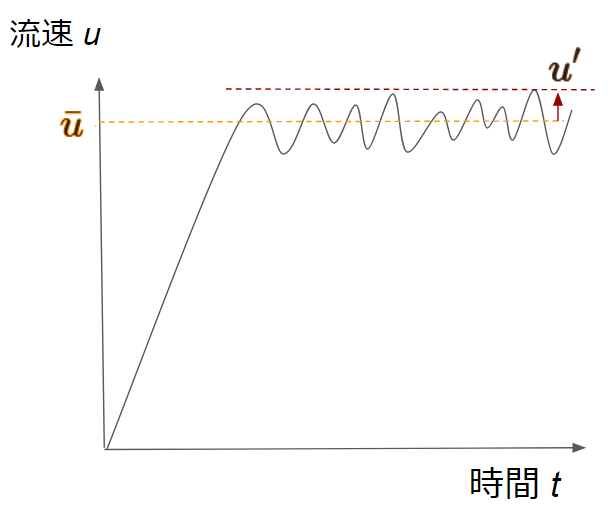
ここで、平均成分を上付きバー、乱れ成分をダッシュで表しています。

各方向の流速と圧力は下記式で表せます。

$$ u = \bar{u} + u’ $$

$$ u = \bar{v} + v’ $$

$$ u = \bar{w} + w’ $$

$$ u = \bar{p} + p’ $$

ここで、乱流成分の平均値はゼロになります。

$$ \bar{u’} = \bar{v’} = \bar{w’} = 0 $$

乱れ成分の瞬時値には特に意味は無いため、乱れ成分の大きさは一般的には統計量（二乗平均平方根）で評価します。

$$ ( \sqrt{\bar{u’^2}} , \sqrt{\bar{v’^2}} , \sqrt{\bar{w’^2}} )$$

レイノルズ応力とレイノルズ方程式

ここまでで乱流を平均成分と乱れ成分に分けることができました。

ここからは成分訳をした形でナビエ・ストークス方程式を書いていきます。

連続の式は平均成分で表せます。

$$ \frac{\partial \bar{u}}{\partial x} = \frac{\partial \bar{v}}{\partial y} = \frac{\partial \bar{w}}{\partial z} = 0 $$

ナビエ・ストークス方程式は下記となります。ここでは簡略化のためx方向のみ示します。

$$\frac{\partial \bar{u}}{\partial t} + \bar{u} \frac{\partial \bar{u}}{\partial x} + \bar{v} \frac{\partial \bar{u}}{\partial y} + \bar{w} \frac{\partial \bar{u}}{\partial z} = – \frac{1}{\rho} \frac{\partial \bar{p}}{\partial x} + \nu (\frac{\partial^2 \bar{u}}{\partial x^2} + \frac{\partial^2 \bar{u}}{\partial y^2} + \frac{\partial^2 \bar{u}}{\partial z^2}) – (\frac{\partial \bar{u’ u’}}{\partial x} + \frac{\partial \bar{v’ v’}}{\partial y} + \frac{\partial \bar{w’ w’}}{\partial z} )$$

これをレイノルズ方程式といいます。

レイノルズ方程式の右辺第３項はレイノルズ応力に関する項で、レイノルズ応力は下記の式で表せます。

$$ \sigma_{Re} = – \rho \left[ \begin{matrix}
\bar{u’ u’} & \bar{v’ u’} & \bar{w’ u’} \\
\bar{u’ v’} & \bar{v’ v’} & \bar{w’ v’} \\
\bar{u’ w’} & \bar{v’ w’} & \bar{w’ w’} \\
\end{matrix}
\right] $$