CFD(Computational Fluid Dynamics)は流体を数値計算によって解く学問です。
流体は世の中にありふれており、CFDは剛体力学などと並んで非常に有用な学問です。しかし、流体力学も難しく、数値計算も難しいため、とっつきにくく中身を完全に理解している人が少ないという問題があります。
また、商用のソフトウェアがあって手軽に結果は得られるので、なんとなくそれらしい結果を見ているものの、その中身を知って妥当性まで検討しているという人は意外と少ないです。
そこで、CFD初心者でもわかる、CFDプログラミングの講座をyoutubeにて公開しました。このコースでは、Pythonを用いて、CFDの基本となる差分法を使って流れの計算を行います。
このコースでは、初めに座学としてナビエストークス方程式を理解し、ナビエストークス方程式を構成する各項についてPythonでプログラミングを行っていきます。
具体的には、移流項、拡散項(粘性項)、圧力項の3つについてそれぞれ計算方法を学ぶことで、最終的にナビエストークス方程式を解くためのスキルを身に着けます。
1次元の計算からはじめて、2次元計算までできる状態を目指します。
本コースで使用するPythonの知識は最低限で大丈夫です。今回使用するライブラリであるnumpyとmatplotlibに関する説明は行いますので、ほとんど知識ゼロの状態でご覧いただいて大丈夫です。
もし不安であれば、下記のPythonコース(全13回)を事前に見ていただくとよいです。プログラミング経験ゼロの方向けに作っているので、環境構築すらできてないとかfor文がわからない方でもCFDを学ぶ準備は整います。
①ナビエ・ストークス方程式 プログラミングの基礎
まずはナビエストークス方程式について理解しましょう。
CFDを行うというのはつまり、ナビエストークス方程式を無理やりコンピュータの力で解くことを意味します。
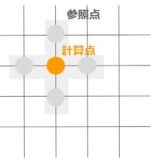
今回はCFDの一種である格子法と呼ばれる手法を用いて計算を行います。
格子法は計算対象を格子状に区切って分割することで、一つ一つの計算対象を簡単化する手法です。
格子法以外には、粒子法と呼ばれる粒子の動きを計算する手法もあります。今回は簡単かつ基本が抑えられる格子法を選びました。
格子法でも粒子法でもCFDを扱うのであれば、計算対象はナビエストークス方程式です。
ナビエストークス方程式は非定常項、移流項、圧力項、粘性項、重力項に分けられます。
今回は特に重要な移流項と圧力項、粘性項に分けて計算を見ていきます。
分割して問題ないかと不安になるかもしれませんが、ナビエストークス方程式をコンピュータで計算する際は、一気に解くという方法はほぼ使われません。
これは、多数の格子に対してナビエストークス方程式を計算しようとすると、大規模な行列計算となってしまうからです。
そのため、CFDではナビエストークス方程式を細かく要素分解して、多少の誤差を許容しながら計算が進められます。
分解して見ることで、それぞれの項の計算もかなり簡単になります。入門としては、最も簡単な考え方である分割する手法を学び、連成手法については追々学んでいくとよいでしょう。
また、本動画ではPythonを忘れてしまった人のために、リスト、numpy、matplotlibについても説明しています。一度Pythonを触ったことがあれば、本動画だけで十分復習になるでしょう。
移流項
移流項 ①移流方程式
ナビエストークス方程式の中で最も重要と言っても過言ではない「移流項」から説明していきます。
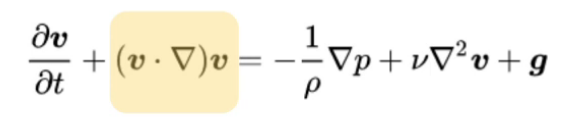
移流項は流体の動きを追跡する項です。対流とも呼ばれます。
移流項は格子法でのみ存在し、粒子法では計算点自体が動くために移流項は存在しません。
格子法において最も難易度の高い計算が、この移流項です。非常に誤差が入りやすく、計算不安定の原因にもなります。
格子法の発展は移流項の計算手法の発展と言っても過言ではないくらいです。難しいかもしれませんが、少しずつ理解していきましょう。
本動画では、移流項の理論部分と今回扱う移流項の離散化スキームについてざっと説明します。
離散化スキームを使うことで、連続的な値に対して空間的に離散化することができます。これはつまり、数学的な微分をコンピュータが扱えるように格子状に分割できるということです。
この分割の補間方法に非常にノウハウが含まれているため、今後数回に渡って詳細を説明していきます。
移流項 ②風上差分
ここからは移流項の離散化スキームについて説明していきます。
適切な離散化スキームを使うことで、格子に分割した計算でも本来の流れを再現することができます。
ここでは、最も簡単で安定的な風上差分について扱います。
風上差分は風上側の値を使って差分を計算します。風上差分は一次精度であり、最も精度の低い離散化スキームです。
風上差分で現れる誤差は拡散として働くため、数値振動を抑える効果があります。
次回説明する中心差分は数値振動を生みますが、これを拡散項により抑えているのが風上差分です。
ここで説明する風上差分は、他の高次の風上スキームと分けて一次風上差分とも呼ばれます。
Pythonの環境を整えてご視聴ください。
移流項 ③中心差分
中心差分は流れに関係なく、周り2点から差分を求める手法です。
風上差分では流れ方向を特定し、風上側を参照する必要がありました。それに対して、中心差分では両側を参照するので、流れ方向の特定が不要です。
風上差分と同じく最もシンプルな離散化スキームの一つであり、中心差分は2次精度であるため一見よさそうに見えます。
しかし中心差分には、数値振動が発生する大きな問題があるため、実用性はありません。
数値振動が発生する理由は簡単で、参照点が両側2点であるために参照点が一つ飛ばしになってしまっていることです。
これにより、格子に沿った流れの変化がとらえきれなくなり、波の形状の急激な変化に対して数値振動を抑えきれなくなります。
中心差分はそのままでは実用性はないですが、これから説明する高次精度の離散化スキームにもつながるので、特徴と課題について理解しておきましょう。
移流項 ④Lax-Wendroff法
Lax-Wendroff法は、2次多項式を使うことで振動を抑制した手法です。
中心差分では精度は高いものの数値振動が問題となりました。そのため、中心差分に対して安定化のための2次の拡散項を加えたのがLax-Wendroff法となります。
Lax-Wendroff法の考え方はシンプルですが、非常に示唆に富んでいます。高次スキームはこのように、高精度化した手法に対して適度に拡散項を加えることで、安定化を図っていくのが基本だからです。
Lax-Wendroff法を基本として、他の移流スキームも学んでいきましょう。
移流項 ⑤二次精度多項式
ここでは二次精度風上差分とQUICKについて説明します。
二次精度風上差分(線形風上差分)は、その名の通り風上差分を二次精度にしたものです。
一次精度の風上差分は2点を使って計算しましたが、二次精度では3点を使って計算を行います。
このように、高次精度にしていく場合は参照点が増えるのが一般的です。
一方でQUICK(Quadratic Upstream Interpolation for Convective Kinematics)も似たような高次精度の手法です。
QUICKは二次精度なのに4点を参照します。これは参照方法が特徴的で、うまく傾きの情報が残るように補間されています。
これらを使えば高次精度となりますが、結果を見ると不安定性に悩まされることは理解できるでしょう。
そこで次回からはただ高次にするだけではない、別の手法を用いた移流計算スキームについて見ていきましょう。
移流項 ⑥CIP法
CIP法(Constrained Interpolation Profile scheme)は、参照点の値と傾き(微分値)を用いて高精度を得る手法です。
傾きの情報が入ることで単純に二倍の情報となるため、波の形状を維持しやすくなります。
さらに参照点が少なくて済むため、数値振動による悪影響も小さくなります。
つまり、CIP法では傾きを使うことにより、多項式高次精度では難しかった精度と安定性のバランスを得ることができます。
デメリットとしては、境界点に微分値を含めないといけなかったり、多次元化した際に非常に複雑な式になるといった問題があります。
ただ、前者の問題は多項式でも似たような問題が起きますし、後者の問題は各次元で分割して計算するということも可能です。
CIP法のメリットに比べると、これらの課題は些細なものです。CIP法は非常に強力なツールであるため、ぜひ理解しておきましょう。
移流項 ⑦TVDスキーム
TVDスキームとは、単調性を維持するためにスキームを変える手法です。
ここでいう単調性とは、時間とともに変動が大きくならないことを意味します。
つまり、波の振動が時間とともに大きくならないように調整しながら離散化スキームを選ぶのがTVDスキームであるとも言えます。
スキームは精度が高いほうが好ましいので、安定性が高い場合には高次精度を使用し、安定性が低い場合は低次で良いのでとにかく数値振動を抑えるスキーマを使用します。
その結果、TVD条件に入るスキームはこれまでに学んできた風上差分やQUICK、中心差分と近いようなスキームをうまく変化させていくことになります。
これにうまく適合するように式を整えたのが、Harten-YeeのNon-MUSCL型TVD法です。
今回はminmod関数によりTVD条件を沿うような関数を作成し、TVDスキームを扱います。
これまでのものと比べると式は複雑ですが、TVDスキームに準拠しているため、波の形状も維持されており、非常に安定性が高いです。
流体解析において不安定性は最大の敵です。まずは計算結果が欲しい場合には、TVDスキームを試すのは最良の方法となりえます。
これよりも高次なものも世の中にあるので、ぜひ興味があればWENOなども調べてみてください。
移流項 ⑧二次元移流方程式
今までは一次元で計算を行っていましたが、ここからは二次元に展開していきます。
二次元になると一気に式の項が増えるため、一見非常に難しそうに見えると思います。しかし、一次元の延長ですので、じっくり理解すれば難しいことはありません。
もしわからなかったら一時停止しながら見てください。
まずは線形対流について学びましょう。
移流項 ⑨非線形移流方程式
線形対流について学んだため、次は非線形対流について扱います。
今までは誤差をわかりやすく表示するために線形対流として学んできましたが、実際のナビエ・ストークス方程式では非線形の形で対流項が現れます。
ぜひ非線形で理解しておきましょう。
移流項 ⑩二次元非線形移流方程式
一次元の非線形方程式を扱ったため、二次元についても学んでおきましょう。
プログラムが非常に長いですが、諦めずに理解していきましょう。
粘性項
粘性項 ①拡散方程式
ここからはナビエ・ストークス方程式の拡散項について扱っていきます。
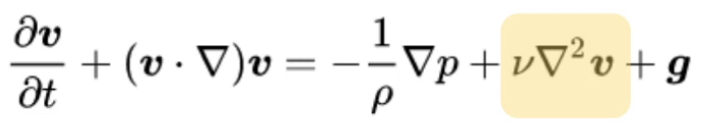
粘性項は周りの流体に対して物性を広げる項です。例えば、一部で流れが早い場合は周囲の遅い流れと平均化されますし、温度も一部が高ければ平均化されます。
このように平均化されていくのが拡散項(粘性項)の特徴です。
その名の通り、流体で言えば粘性を表す項で、粘性とは値が拡散するのと同じ意味ということになります。
拡散方程式では、時間とともに値が広がっていく様子を確認してきましょう。
粘性項 ②陽解法と陰解法
粘性項には拡散数という計算の不安定性を評価する指標があります。
拡散数は時間刻み幅と格子幅により決定され、拡散数を超えると数値振動が発生します。
そのため、粘度の高い流体に対して解像度の高いメッシュを使いたい場合、非常に小さい時間刻みを使わないといけなくなります。
そこで、非常に有効なのが陰解法です。
過去の時間ステップの情報で計算するのが陽解法であるのに対し、現在の時間ステップの情報を用いて計算するのが陰解法です。
現在の時間ステップで計算するため、行列計算が必要となります。
計算が一見難しくなりますが、陰解法を取り入れると時間ステップを気にせず計算することができるようになり、非常に楽になります。
陰解法は非常に便利でよく利用される手法ですので、ぜひ理解しておきましょう。
粘性項 ③二次元拡散方程式
最後は拡散方程式を二次元に展開していきます。
拡散方程式の二次元への展開は意外と簡単です。それはxy方向で同じ値となるためです。
そのため、今回はx方向流速のみ計算します。
プログラムは少し長くなるため丁寧に説明しますが、分かる部分は飛ばしてもらって構いません。
圧力項
圧力項 ①圧力項とMAC法(Marker And Cell Method)
ここからはナビエ・ストークス方程式の圧力項について見ていきます。
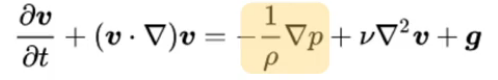
圧力はナビエ・ストークス方程式の中でも非常に難しい項です。
ナビエ・ストークス方程式には解がないため、ひと工夫しないと計算できません。その際に、ナビエ・ストークス方程式と分けて計算されるのが圧力項です。
つまり、圧力を求める式と圧力を除いたナビエ・ストークス方程式の2つを計算することになります。この手法をMAC法(Marker And Cell Method)と呼びます。
今回はこのMAC法を使って計算を行います。
圧力項を除いたナビエ・ストークス方程式は今までの移流項と拡散項の計算で問題なく行えるため、ここでは圧力計算のためのポアソン方程式について学んでいきましょう。
圧力項 ②ラプラス方程式
ラプラス方程式は、ポアソン方程式のソース項のない式のことを指します。
つまり、ほとんどポアソン方程式(MAC法で使用する式)と同じです。
ラプラス方程式は圧力の平衡状態を求める式です。計算領域の端となる境界条件を設定し、ループ計算を行います。
平衡状態の計算結果は、布をピンと張ったようなイメージです。
今までのように時間進行しない計算なので、ぜひその辺りの違いに着目しておくと良いでしょう。
圧力項 ③境界条件とポアソン方程式
ここでは境界条件の値を変更した場合とソース項を入れた場合の計算結果について見ていきます。
ラプラス方程式にソース項を与えたものがポアソン方程式です。
ただ、ソース項を入れても難しさは大きく変わらないため、まとめて見ておきましょう。
圧力項 ④収束性の評価
圧力計算では平衡状態の計算を行うため、収束性が重要になります。
収束性が悪いと誤差が小さくなるまでに非常に計算時間が長くなりますし、途中で打ち切ってしまうと計算結果に誤差が残ります。
まずは圧力計算とその収束性の評価方法について理解しましょう。
圧力項 ⑤ガウスザイデル法
前回説明したように、圧力計算では収束性が重要であり、収束性の高い行列解法が好まれます。
その一つがガウスザイデル法です。
ヤコビの反復法よりもガウスザイデル法の収束性が高いです。ここでは2つを比較して評価します。
圧力項 ⑥SOR法(Successive Over Relaxation Method)
ガウスザイデル法よりも収束性が高いと言われているのが、SOR法です。
SOR法はガウスザイデル法に対して過緩和を与えることで、収束性を高める手法です。
圧力計算で一般的に使われるのは、ガウスザイデル法とSOR法です。SOR法は過緩和を使うため直感的に少し理解し難いですが、よく利用されるためぜひ知っておきましょう。
おわりに
今回はCFDのプログラミングについて動画で説明しました。
特に、ナビエストークス方程式の重要な項についてそれぞれ章を立てて、重要な順で説明しています。
格子法で流体解析をする場合は、移流項が厄介です。計算不安定と誤差は移流項から引き起こされる場合が多く、かつ手法がたくさんあるので混乱しがちです。
今回紹介した手法以外にも精度の高い手法はたくさんありますが、基本は押さえているので今後さらに高精度な手法と出会っても理解しやすいと思います。
ぜひこの動画を思い出してください。
今回使用した手法は格子法でしたが、CFDの手法には他にも色々あります。例えば粒子法などです。
もし機会があればそちらについても紹介したいと思います。ぜひご期待のほど。
 ITとCFD入門サイト
ITとCFD入門サイト