【LBM】非ニュートン性流体【格子ボルツマン法講座 #12】

はじめて格子ボルツマン法を学ぶ初心者のための講座、第１２回になります。

格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。

全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD（流体解析）の手法を知っておくとベターです。

前回は無次元で定義されている格子ボルツマン法の有次元化 について説明しました。有次元化することで、現実世界の現象を解析できるようになります。詳しくは下記からどうぞ。

今回は、非ニュートン性流体について紹介します。

非ニュートン性

今までは動粘度を定数として扱うニュートン流体を対象としていました。

そのため動粘度が変化しないので、初期値として宣言すれば後から修正は不要でした。

ここからは動粘度が変化する「非ニュートン流体」について扱っていきます。

非ニュートン流体とは？

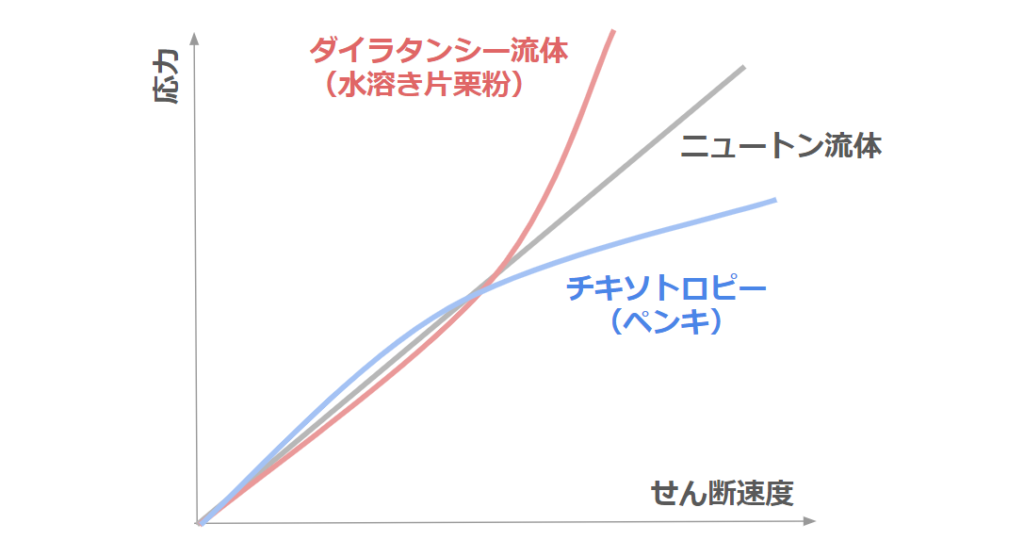
非ニュートン流体とは、せん断速度に応じて粘度の変化する流体です。

例えば、ペンキはせん断がかかると粘度が低下する性質があり、塗りやすさと付着性を併せ持っています。

逆に水溶き片栗粉は、混ぜると固体化する特徴があり、せん断がかかると固くなります。

樹脂なども非ニュートン流体であり、世の中には多くの非ニュートン流体が存在します。

粘度の変化は物体によりますが、共通するのは「せん断速度により粘度が変化すること」です。

格子ボルツマン法と非ニュートン流体

格子ボルツマン法で非ニュートン流体を計算する場合、粘度の計算を計算ループ内に移動させます。

ここからは実装の順に説明します。

非ニュートン性の計算でまず行うのは、せん断速度の計算です。

マクロの流速を用いると、ひずみテンソルは下記の式で得られます。

$$ S_{\alpha \beta} = \frac{1}{2} ( \frac{\partial u_x}{ \partial y} + \frac{\partial u_y}{ \partial x} ) $$

上の式だと連続的な式になっているので、プログラムに落とす際には離散化が必要です。

離散化を行うと下記の式になります。

$$ S_{\alpha \beta} \simeq \frac{1}{2} ( \frac{u_x [i + 1] [ j ] – u_x [i – 1] [ j ] }{ \Delta y} + \frac{u_y [i] [ j + 1] – u_y [i] [ j – 1 ] }{ \Delta x} ) $$

マクロな値を使うと上記のようになります。

中心差分で求めているので、ステンシル（アクセスする計算点）が大きいのが不便です。

そこで、格子ボルツマン法のミクロ量を使用したひずみテンソルの計算法もあります。

$$ S_{\alpha \beta} = – \frac{3}{2 \tau} \sum f^{(1)} c_{ix} c_{iy} $$

$f^{(1)}$は摂動展開のクヌーセン数１次の項です。直接計算できないため、下記の非平衡分布で近似します。

$$ f^{(1)} \approx f^{neq} = f – f^{eq}$$

乱流のような流れだと誤差が出やすいですが、単純な流れであれば近似によりひずみテンソルの計算式が下記になります。

$$ S_{\alpha \beta} \approx – \frac{3}{2 \tau} \sum (f – f^{eq}) c_{ix} c_{iy} $$

次にひずみテンソルからせん断速度テンソルを計算します。

$$ \dot{\gamma}_ {\alpha \beta} = \sqrt{ S_{\alpha \beta} S_{\alpha \beta} } $$

最後に動粘度を計算します。

様々な粘度モデルがありますが、ここではよく使われるpower-lawモデルを紹介します。

power-lawモデルは下記で計算されます。

$$ \nu (\dot{\gamma}) = m | \dot{\gamma} |^{n-1} $$

mとnはフィッティングパラメータです。n=1のとき、ニュートン流体になります。

これらの計算を、プログラムの計算ループ内で行うことで、格子ボルツマン法で非ニュートン流体の計算を行うことができるようになります。

おわりに

今回はpower-lawモデルを使用した非ニュートン流体について紹介しました。

重要なポイントは下記のとおりです。

• 非ニュートン流体は、せん断速度により粘度が変化する
• 格子ボルツマン法の計算ループ内で粘度を変化させる
• マクロ値でせん断速度を計算すると、ステンシルが大きくなる
• 粒子速度からせん断速度を計算することもできる
• power-lawモデルなどを使うことで、せん断速度から粘度変化を与えられる

世の中の様々な流体は非ニュートン流体です。難しい内容ではないので、ぜひ理解しておきましょう。

次回は初心に戻って、格子ボルツマン法と格子ガスオートマトン法について説明します。

格子ボルツマン法は格子ガスオートマトン法を流体に適用したものです。格子ガスオートマトン法と格子ボルツマン法の違いを知ることで、格子ボルツマン法の重要なポイントを理解することができます。

また、元の手法を知ることで、ナビエストークス方程式と大きく異なることも理解しやすくなるでしょう。