はじめて格子ボルツマン法を学ぶ初心者のための講座、第10回になります。
格子ボルツマン法は歴史が浅いこともあり、まだ情報が少ないのが正直なところです。そこで、本サイトでは、ゼロからでも理解できるように丁寧に進めていくようにします。数学的な部分も極力簡単にするので、ぜひ最後までついてきていただけると幸いです。
全く知識のない人でも一応理解できるように説明しますが、可能であればナビエストークス方程式やほかのCFD(流体解析)の手法を知っておくとベターです。
前回は 流入・流出境界条件 について説明しました。下記からどうぞ。
今回は、特殊な壁面境界条件であるインターポレイテッドバウンスバックについて紹介します。
インターポレイテッドバウンスバック
ここでは、高度な壁面境界について紹介します。
壁面境界として、ハーフウェイバウンスバックとオングリッドバウンスバックを紹介しました。しかし、それぞれ「格子点の中間」と「格子上」にしか壁を配置できません。
そのため、格子に沿ったギザギザの壁しか表現できず、曲面に対応できません。
そこで考案されたのが、インターポレイテッドバウンスバックです。
その名の通り、「補間」により格子点間の任意の位置の壁を表現する方法です。
インターポレイテッドバウンスバックでは、壁の位置を示す変数$q$を導入します。
壁は端の格子点より外側にあると考え、変数$q$がゼロだと格子点上に壁があり、$q=1$だと1格子分離れた位置に壁があると考えます。
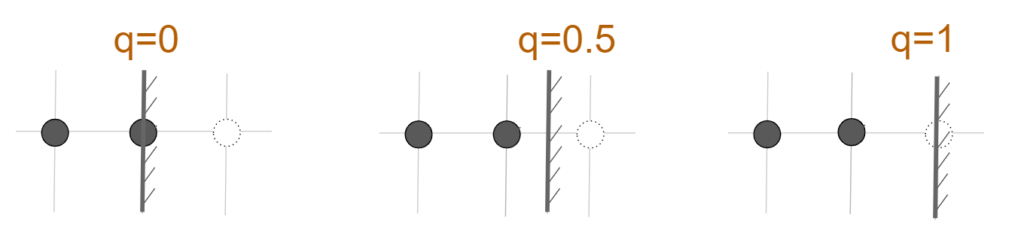
つまり、変数$q$次第でオングリッドバウンスバックとハーフウェイバウンスバックを満たすような補間式が出来上がることになります。
インターポレイテッドバウンスバックでは、変数$q$が$q = 0 ~ 0.5$までの場合と、$q = 0.5 ~ 1$までの場合で分けて考えます。
まずは$q = 0 ~ 0.5$までの場合について考えましょう。
q = 0 ~ 0.5(q < 0.5)
$ q = 0 ~ 0.5$とはつまり、格子点が壁に近い状態のことです。
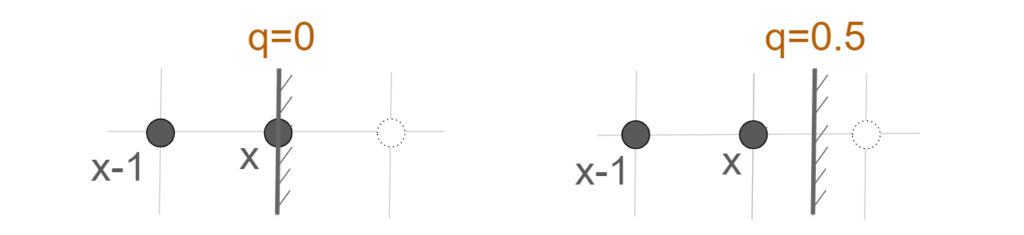
粒子は1ステップで1格子分だけ移動するので、反射後にx点に到達する粒子は、反射前はx-1とxの間にいたことになります。
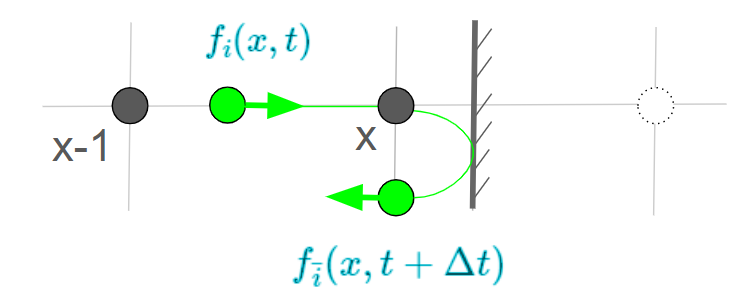
つまり、反射前の$f_i (t)$の値を求めることで、x点上の反射後の値を求めることができます。
反射前の $f_i (t)$ はx-1とx点の値の補間で求められます。
$$ f_i (x,t) = (1-2q) f_i (x-1,t) + 2q f_i (x,t) $$
あとは上の式をバウンスバックにより移動後のx点の値を求めるだけです。
$$ f_{\bar{i}} (x,t + \Delta t) = (1-2q) f_i (x-1,t) + 2q f_i (x,t) – 2 w_i \rho \frac{c_i u}{c_s^2} $$
最後の項は壁面速度なので、固定壁の場合は不要となります。
q > 0.5
次に、$q$が$q = 0.5 ~ 1$、つまり壁が格子点から離れている場合を考えましょう。
先ほどの条件と大きく異なるのは、反射前の粒子がx-1とxの間にいないことです。
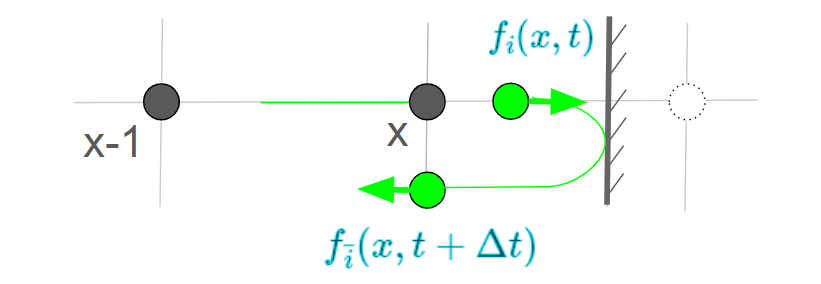
よって、$q < 0.5$と同じ方法では、x点の反射後の分布関数を求めることができません。
そこで考え方を変えて、「反射前の値を補完で求める」だったものを「反射後の値を補完で求める」に変更します。
すると、x点の反射後の値はx-1点と$f_i (t)$のある点の補間により求めることができます。
反sy前の粒子位置を仮に$\hat{x}$とすると、下記の図のようになります。
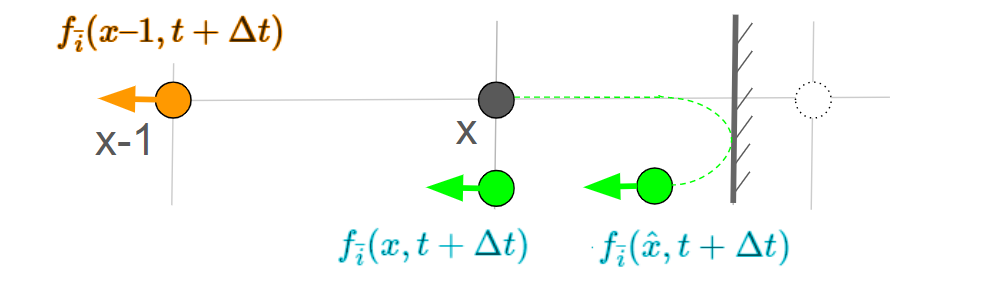
よって、x点の補間式は下記となります。
$$ f_{\bar{i}} (x,t + \Delta t) = \frac{1}{2q} f_{\bar{i}} (\hat{x}, t + \Delta t ) + \frac{2q – 1}{2q} f_{\bar{i}} (x – 1, t + \Delta t ) $$
$f_i (\hat{x}, t)$は $f_i (x, t)$ から$\Delta t$進んだ点であるため、下記で求められます。
$$ f_i (\hat{x}, t) = f_i (x, t) – 2 w_i \rho \frac{c_i u}{c_s^2} $$
よって、$f_i (\hat{x} , t + \Delta t)$を代入すると、$q > 0.5$ の場合の式が得られます。
$$ f_{\bar{i}} (x,t + \Delta t) = \frac{1}{2q} f_i (x, t) + \frac{2q – 1}{2q} f_{\bar{i}} (x – 1, t + \Delta t ) – 2 w_i \rho \frac{c_i u}{c_s^2} $$
まとめ
以上をまとめると、インターポレイテッドバウンスバックの壁面条件は下記の2つの式で求められます。
$q \leq 0.5$のとき:
$$ f_{\bar{i}} (x,t + \Delta t) = (1-2q) f_i (x-1,t) + 2q f_i (x,t) – 2 w_i \rho \frac{c_i u}{c_s^2} $$
$q > 0.5$のとき:
$$ f_{\bar{i}} (x,t + \Delta t) = \frac{1}{2q} f_i (x, t) + \frac{2q – 1}{2q} f_{\bar{i}} (x – 1, t + \Delta t ) – 2 w_i \rho \frac{c_i u}{c_s^2} $$
反射前と反射後の値を混同しないように注意しましょう。
おわりに
今回はインターポレイテッドバウンスバックについて紹介しました。
インターポレイテッドバウンスバックの重要なポイントは下記の通りです。
- 補間により任意の壁を表現できる
- q=0でオングリッド、q=0.5でハーフウェイバウンスバックになる
- q=0.5を境に、補間の仕方が変わる
構造格子しか扱えない格子ボルツマン法において、インターポレイテッドバウンスバックはほぼ必須な境界条件です。ぜひ理解しておきましょう。
次回は、格子ボルツマン法の無次元化と有次元化について説明します。
格子ボルツマン法は特殊であり、無次元で計算されます。よって、何も考えないと無次元で全て表現されてしまいます。
そこで、次回は有次元にする場合について説明したいと思います。
 ITとCFD入門サイト
ITとCFD入門サイト 

