特性曲線法を使うことで、下記の偏微分方程式を解くことができます。
$$ a (x,y,z) \frac{\partial z}{ \partial x } + b (x,y,z) \frac{\partial z}{ \partial y } = c (x,y,z) $$
これは、CFDにも適用することができます。
移流方程式
格子法において、移流項の計算は最も難しいとされています。これは、差分法では計算安定性と誤差のバランスが上手く取れないためです。
移流方程式は下記の式で表されます。
$$ \frac{\partial v}{\partial t} + v \frac{\partial v}{\partial x} = 0$$
時間tと空間xによって、流速vが輸送されます。
特性曲線法の移流方程式への適用
先述の通り、特性曲線法は下記で表せます。
$$ a (x,y,z) \frac{\partial z}{ \partial x } + b (x,y,z) \frac{\partial z}{ \partial y } = c (x,y,z) $$
下記を代入することで、移流方程式に変換できます。
$$ a = 1$$
$$ b = v$$
$$ x = t $$
$$ y= x $$
$$ z = v(x,t)$$
つまり、特性曲線法を移流方程式に適用できることがわかります。
特性曲線法
ここからは特性曲線法について説明します。
$$ a (x,y,z) \frac{\partial z}{ \partial x } + b (x,y,z) \frac{\partial z}{ \partial y } = c (x,y,z) $$
上記の偏微分方程式をそのまま解くことはできないので、常微分方程式に変換します。下記の式を特性方程式と言います。
$$ \frac{\partial x(t)}{ \partial t } = a (x,y,z)$$
$$ \frac{\partial y(t)}{ \partial t } = b (x,y,z)$$
連鎖則(チェーンルール)$ \frac{dz}{dt} = \frac{dz}{dx} \frac{dx}{dt} + \frac{dz}{dy} \frac{dy}{dt} $より、下記が導けます。
$$ \frac{\partial z(t)}{ \partial t } = c (x,y,z)$$
曲面
特性曲線法では、解曲面を考えます。
イメージ図をかきに示します。図と式を見比べながら読み進めてください。
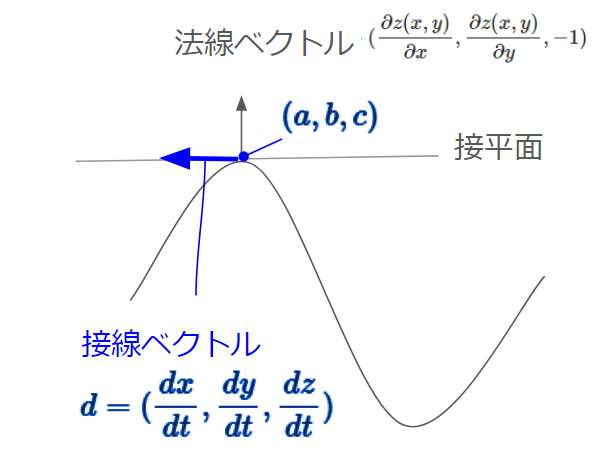
対象の式の解曲面の法線ベクトルは下記で表せます。
$$ (\frac{\partial z (x,y)}{ \partial x} , \frac{\partial z (x,y)}{ \partial y} , -1) $$
ベクトル場$(a,b,c)$に対して、法線ベクトルの内積を取ると、対象の偏微分方程式を復元できます。
$$ (a,b,c) \cdot (\frac{\partial z (x,y)}{ \partial x} , \frac{\partial z (x,y)}{ \partial y} , -1) = a (x,y,z) \frac{\partial z}{ \partial x } + b (x,y,z) \frac{\partial z}{ \partial y } – c (x,y,z) = 0$$
ここで、接線ベクトルdは変数tを用いて下記で表せます。
$$ d = ( \frac{dx}{dt} , \frac{dy}{dt} , \frac{dz}{dt} )$$
今までの説明を図で示すと下記のようになります。
接線ベクトルは接平面と並行なので、定数kを用いて下記の式が導けます。
$$\frac{dx}{ dt} = ka (x,y,z) $$
$$\frac{dy}{ dt} = kb (x,y,z) $$
$$\frac{dz}{ dt} = kc (x,y,z) $$
よって、下記の式が導けます。
$$\frac{dx}{a(x,y,z)} = \frac{dy}{b(x,y,z)} = \frac{dz}{c(x,y,z)} $$
左側・右側の式だけで計算すると、xyの積分から積分定数$C_1$、yzの積分から積分定数$C_2$が得られます。
それらの積分定数に対して、$C_2 = f(C_1)$のように関数fの関係で表せるとすると、下記の式が得られる。
$$ z = f (<xとyの式>)$$
fはどんな関数でもよく、境界値を指定することで定まります。
実践
例えば、下記の移流方程式を解くことにします。
$$ \frac{\partial v (x,t)}{\partial t} + v \frac{\partial v (x,t) }{\partial x} = 0$$
特性曲線法を適用すると下記が得られます。
$$ \frac{dx}{1} = \frac{dy}{1} = \frac{dv}{0} $$
xとyの式を積分すると、下記が得られます。
$$ y – x = C_1$$
次にvの式ですが、分子は必ず0なので、$dv=0$より、$v=C_2$となります。
$C_2$と$C_1$は関数fの関係で表せるため、$ C_2 = f(C_1)$より、下記が得られます。
$$ v(x,t) = f(y – x) $$
関数fはこの段階では自由に決められます。関数を一意に定めるためには、境界条件を決める必要があります。
おわりに
今回は、特性曲線法で移流方程式を解く方法について解説しました。
特性曲線法は、偏微分方程式を常微分方程式に変換して解きます。数学的な操作が多くて理解しにくいと思うので、ぜひイメージ図だけでも覚えておきましょう。
yotubeでも解説しています。
youtubeでも色々動画を出しています。こちらもどうぞ。
 ITとCFD入門サイト
ITとCFD入門サイト 

